| Главная Научный калькулятор | |
|
|
Задача №224Биссектриса угла В пересекает сторону АС треугольника АВС в точке М и делит её на отрезки АМ=21 и СМ=27. Найти периметр АВС, если биссектриса угла АМВ перпендикулярна АВ.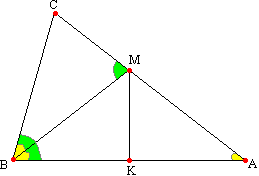 Воспользуемся вот такой теоремой: если в произвольном треугольнике две из указанных четырех линий (высота, медиана, биссектриса, ось симметрии) совпадут, то такой треугольник будет равнобедренным (а значит, совпадут и все четыре линии). В треугольнике АМВ прямая МК является биссектрисой и высотой по данным, поэтому треугольник АМВ равнобедренный. АМ=МВ=21. Теорема: в равнобедренном треугольнике углы при основании равны. Обозначим этот угол за α, тогда ∠АВС=2α. Теорема: внешний угол треугольника равен сумме двух внутренних несмежных с ним. Поэтому ∠ВМС=2α. Мы видим, что в треугольниках АВС и ВМС равны по два угла, поэтому они подобны. Откуда (зная, что АС=АМ+МС=48): 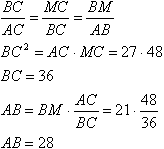 Р=АВ+ВС+АС=28+36+48=112 |