| Главная Научный калькулятор | |
|
|
Задача №239В треугольнике ABC точки F и H - основания высот, опущенных соответственно из вершин A и B. Точка О - центр описанной окружности. Прямая FH пересеается с прямой OC в точке K. Найдите радиус описанной окружности, если известно, что BC=a, FK=b, CK=m.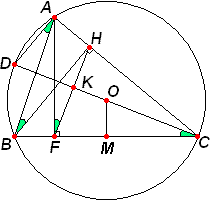 1. Докажем, что прямая СО перпендикулярна HF. Проведем диаметр CD. Углы BCD и BAD равны, т.к. опираются на одну дугу. Т.к. AD перпендикулярна АС. Угол DAC опирается на диаметр, поэтому он равен 90 градусов, т.е. AD^AC, а значит, AD||BH, и следовательно ∠ВАD=∠ABH как внутренние накрест лежащие. У прямоугольный треугольников АВF и АВH общая гипотенуза. Известно, что центр описанной около прямоугольного треугольника окружности лежит на середине его гипотенузы, а ридиус равен её половине. Поэтому около этих двух прямоугольных треугольников АВF и АВH описана одна окружность, т.е. точки А, В, F и H лежат на одной окружности с диаметром АВ, в силу чего ∠АВН=∠АFH. Таким образом, ∠ВСD=∠AFH. Отсюда ∠KFC=90°-∠AFH=90°-∠BCD. Используем теорему о сумме углов треугольника: ∠СКF=180°-∠ВСD-∠KFC=180°-∠ВСD-90°+∠BCD=90°, т.е. СD^HF, что и требовалось доказать. Случай, когда треугольник АВС тупоугольный рассматривается аналогично и имеет такой же результат. 2. Рассмотрим прямоугольный треугольник FKC. Опрежелим гипотенузу по теореме Пифагора: FC2=FK2+CK2=b2+m2 Из точки О опустим перпендикуляр ОМ на ВС. Как известно центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляром, поэтому МС=а/2. Прямоугольные треугольники FKC и OMC подобны (у них угол С общий), поэтому: 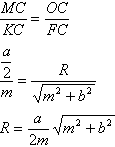
|