| Главная Научный калькулятор | |
|
|
Задача №244Основание пирамиды - ромб, большая диагональ которого равна 2d и острый угол равен α. Все боковые грани составляют с плоскостью основания углы β. Найти объём пирамиды!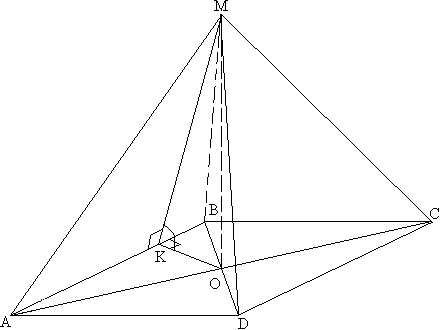 Пусть большая диагональ ромба - АС, а значит острыми углами будут А и С (противоположные углы ромба равны). Вспомним свойства диагоналей ромба: Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся попалам. Диагонали ромба являются биссектрисами его углов. Т.е. АО=ОС=d и ∠ВАО=∠DAO=α/2 Рассмотрим прямоугольный треугольник АОВ. В нем: ОВ=ОА*tgα/2, следовательно BD=2ОВ=2ОА * tgα/2=2d * tgα/2 SABCD=1/2 * AC * BD=1/2 * 2d * 2d * tgα/2=4d2 * tgα/2 Из точки О опустим перпендикуляр ОК на АВ. Теперь соединим точку К и вершиной пирамиды. МК перпендикулярна АВ по теореме о трех перпендикулярах. Значит, угол МКО является линейным углом двугранного угла между боковой гранью АВМ и основанием АВСD и равен β. Из прямоугольного треугольника АОК найдем: ОК=АО * sin∠ВАО=d * sinα/2 Изпользуя теорему: Если все боковые грани пирамиды наклонены к плоскости основания под одинаковым углом, то в основание такой пирамиды можно вписать круг, а высота, опущенная из вершины на основание, падает в центр вписанного в основание круга. Центром вписанного в ромб круга является пересечение его диагоналей. Поэтому МО есть высота пирамиды. МО перпендикулярна любой прямой в плоскости основания АВСD по определению в том числе и ОК. Из прямоугольного треугольника МОК найдем: МО=ОК * tgβ=d * sinα/2 * tgβ Осталось подставить найденные значения в формулу объема пирамиды 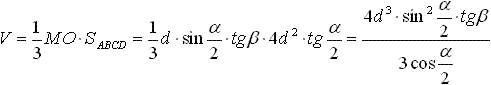
|