| Главная Научный калькулятор | |
|
|
Задача №245Квадрат и ромб, не являющийся квадратом, имеют одинаковые периметры. Найдите острый угол ромба, если площадь его равна половине площади квадрата.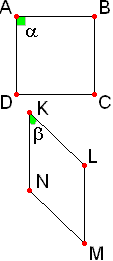 1. Для решения этой задачи нам необходимо будет вспомнить теорему 44 из темы Квадрат.
Запишем их соответственно:
1. Для решения этой задачи нам необходимо будет вспомнить теорему 44 из темы Квадрат.
Запишем их соответственно:SABCD=AB2 (1) SKLMN=KL2 * sinβ (2) 2. Что же означает тот факт, что периметры этих четырехугольников равны? А примерно следующее: РABCD=РKLMN 4АВ=4KL АВ=KL (3), т.е. стороны этих плоских фигур равны. 3. Запишем данное нам отношение между площадьми ромба и квадрата: SABCD=2SKLMN Воспользуемся выражениями (1) и (2) AB2=2KL2 * sinβ А теперь выражением (3) с пометкой на то, что квадраты равных чисел равны AB2=2AB2 * sinβ Поделим это выражение на 2AB2, получим: sinβ=1/2 Рb=arcsin(1/2) Т.к. нам требуется найти острый угол ромба, то принимаем β=30°. |