| Главная Научный калькулятор | |
|
|
Задача №26Стороны оснований правильной треугольной усеченной пирамиды равны б см и 12 см. Угол между плоскостями боковой грани и основания равен 30. Найдите площадь боковой поверхности данной усеченной пирамиды.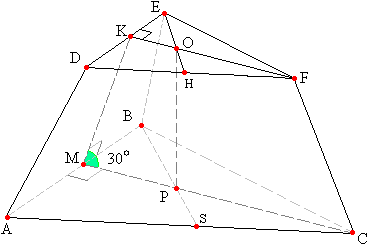 Через ребро CF перпендикулярно ребрам АВ и DE (они параллельны) проведем плоскость. Эта плоскость пересечет основания по высотам СМ и FK соответственно большое и маленькое. Боковую грань ADEB эта плоскость пересечет по апофеме МК. Ребро АВ перпендикулярно построенной плоскости, поэтому оно перпендикулярно и любой прямой этой плоскости (по определению перпендикуляра к плоскости). Т.е. АВ^МК и АВ^МС, поэтому угол КМС является линейным углом двугранного угла между боковой гранью и основанием равен 30°.
Через ребро CF перпендикулярно ребрам АВ и DE (они параллельны) проведем плоскость. Эта плоскость пересечет основания по высотам СМ и FK соответственно большое и маленькое. Боковую грань ADEB эта плоскость пересечет по апофеме МК. Ребро АВ перпендикулярно построенной плоскости, поэтому оно перпендикулярно и любой прямой этой плоскости (по определению перпендикуляра к плоскости). Т.е. АВ^МК и АВ^МС, поэтому угол КМС является линейным углом двугранного угла между боковой гранью и основанием равен 30°.Через ребро BE перпендикулярно ребрам АC и DF (они параллельны) проведем плоскость. Эта плоскость также пересечет основания по высотам. Как первая, так и вторая построенные нам плоскости перпендикулярны основаниям по теорему: если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то это перпендикуляр полностью лежит в первой плоскости. Поэтому проведенный нами перпендикуляр должен лежать как в плоскости МКFC, так и в плоскости ВЕНS. Т.е. этот перпендикуляр принадлежит линии пересечения этих плоскостей и упадет на пересечение высот большего основания. Как известно пирамида правильная, т.е. основания правильные треугольники. В правильно треугольнике высоты совпадают с медианами, поэтому, находя отрезки КО и МР можно применить такую теорему: медианы треугольника пересекаются в одной точке и точкой пересечения делят друг друга в отношении 2:1, считая от вершины. Итак, 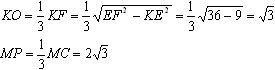 Вычертим трапецию МКОР: 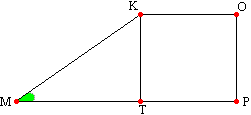 Проведем высоту КТ. Найдем МК:
Проведем высоту КТ. Найдем МК: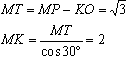 Пирамида у нас правильная, поэтому все боковые грани суть равные равнобедренные трапеции. Пользуясь этим, найдем площадь боковой поверхности: 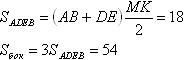
|