Задача №34

Через точки А и В, лежащие на плоскости α (альфа), проведены два параллельных отрезка АС=12 и ВD=8, нележащих в плоскости α. Прямая СD пересекает плоскость α в точке К. Найти площадь треугольника КВD, если ВК=10, СD=4 и ∠DКВ=45°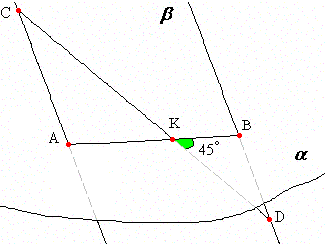

Через прямые АС и BD проведем плоскость β (параллельные прямые определяют плоскость и притом только одну). Плоскости α и β пересекаются по прямой АВ. Точка К прямой СD тоже лежит на прямой АВ, т.к. принадлежит и плоскости α и плоскости β.
Рассмотрим треугольники АСК и КВD. Они подобны по двум углам (∠АКС=∠ВКD - вертикальные, ∠САК=∠КВD - внутренние накрестлежащие при параллеьных прямых АС и BD и секущей АВ). Поэтому в них равны отношения соответственных отрезков: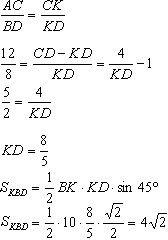