| Главная Научный калькулятор | |
|
|
Задача №88К окружности с центром в точке О и радиусом 6 см из точки А проведены две касательные. Найдите угол между этими касательными, если ОА = 4 корня из 3 см.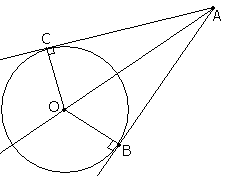 Теорема.Радиус, проведенный в точку касания прямой окружности, перпендикулярен этой прямой (касательной). Из этой теоремы следует, что треугольники АОВ и АОС прямоугольные и еще они равны по катету и гипотенузе (ОС = ОВ - как радиусы, а АО - общая). Значит, АО делит искомый угол САВ на два равных угла. Найдем один из них с помощью связи сторон и тригонометрических функций в прямоугольном треугольнике: sin∠ОАС = ОС/OА = √3/2 (корень из 3 попалам) ∠ОАС = 60о ∠ВАС = 2∠ОАС = 120о |