| Главная Научный калькулятор | |
|
|
Задача №92Докажите, что прямая, проходящая через середины двух противоположных рёбер правильного тетраэдра, перпендикулярна к ним. Найдите длину отрезка, соединяющего середины противоположных рёбер правильного тетраэдра, если ребро тетраэдра равно 1 м.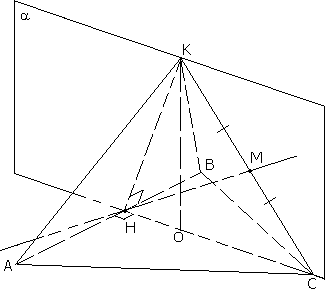 Определение. Все грани правильного тетраэдра есть правильные треугольники. Через ребро КС и точку Н проведем плоскость α. Наша прямая НМ принадлежит этой плоскости т.к. имеет ней две общие точки Н и Мю Эта плоскость пересечет плоскость АВС по прямой СН. Точка Н - середина АВ, поэтому СН есть медиана треугольника АВС, а следовательно и высота - АВ^СН. Соединим точки К и Н. КН перпендикулярна АВ по теореме о трех перпендикулярах. АВ перпендикулярна двум пересекающимся прямым КН и НС плоскости КНС, и поэтому она перпендикулярна всей плоскости или любой прямой этой плоскости. Значит, АВ^НМ Рассмотрим треугольник НКС. В нем КН=НС (это высоты в равных правильных треугольниках). Значит треугольника НКС равнобедренный, причем НМ есть медиана проведенная к основанию. Теорема. В равнобедренном треугольнике медиана проведенная к основанию является также и высотой. Значит МН^КС Для находения НМ рассмотрим треугольник КНМ. Он прямоугольный и КМ есть половони КС - КМ=1/2 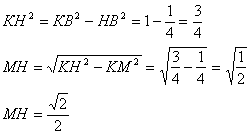
|