| Главная Научный калькулятор | |
|
|
Задача №96Дана окружностьи и в ней хорда равна 90 см, расстояние от центра хорды до верха окружности 9,5 см. Найти радиус окружности.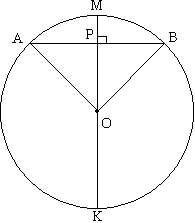 Теорема. Диаметр, проведенный через центр хорды, перпендикулярен ей и делит её попалам. Поэтому диамметр, проведенный через точку Р перпендикулярен хорде АВ, а следовательно совпадает с МР. Пусть АО=ВО=МО=R, тогда ОР = R - 9,5. В прямоугольном треугольнике ОРВ запишем теорему Пифагора: OB2 = OP2 + PB2 R2 = (R-9,5)2 + 452 19R=7739/4 R=7739/76 |