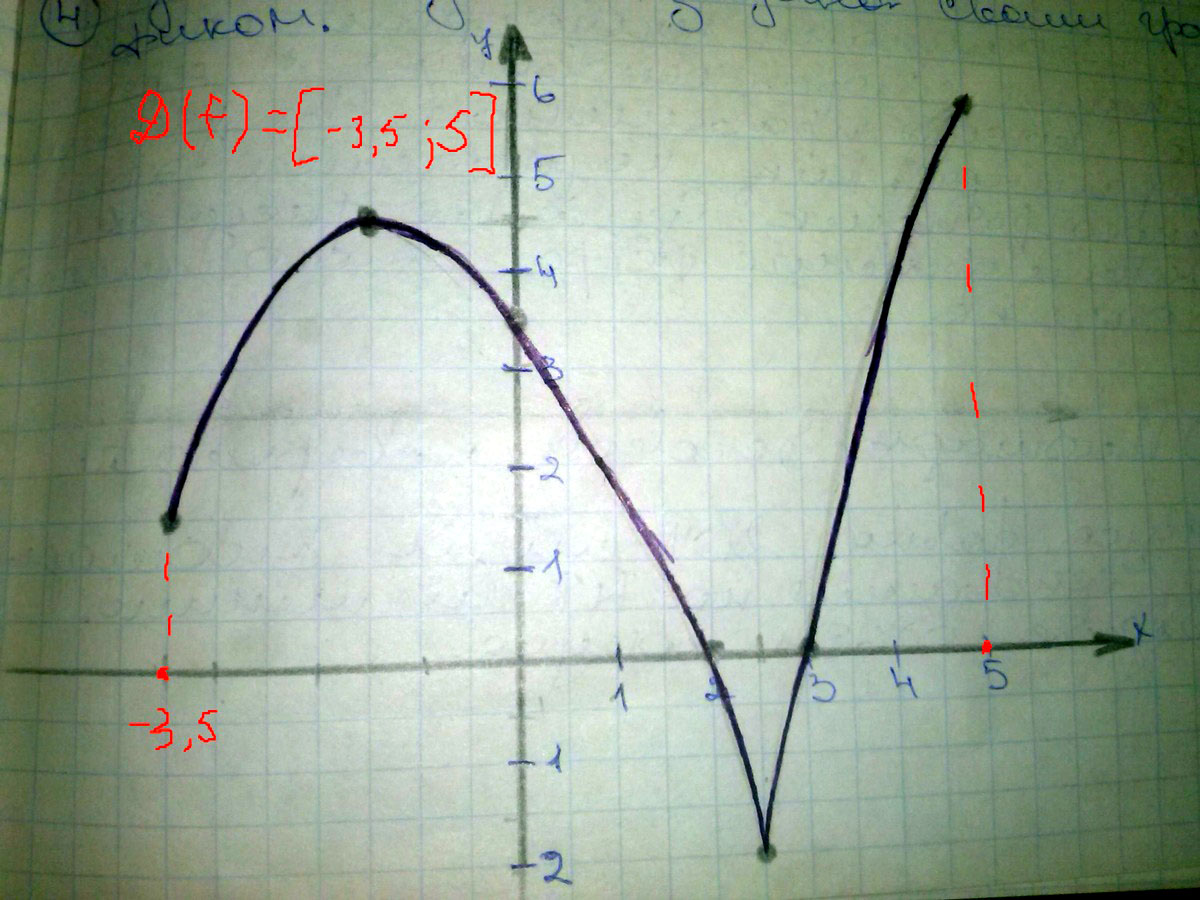
Функция y=f(x) задана своим графиком.
Укажите:
1) область определения функции.
2) при каких значениях x f(x) > 3,5.
3) при каких значениях x f'(x) < 0, f'(x) > 0
4) в каких точках касательные к нему параллельны оси абсцисс.
5) наибольшие и наименьшие значения функции.

1) Область определения - промежутки, на которых у функции есть значение. В нашем случае нам нужно выбрать промежутки на оси абсцисс (горизонтальной оси), потому что именно они задают всевозможные значения аргумента х. Для данной функции область определения будет записана таким промежутком: [-3,5 ; 5]. Квадратные скобки потому, что крайние точки включены в область определения (то есть, значение функции в этих точках определено).

2) Откладываем точку на оси ординат (вертикальная ось), равную 3,5. Дальше проводим через нее прямую, параллельную другой оси. Смотрим, на каких промежутках график находится выше построенной прямой. Он будет выше на промежутках (-2,75 ; 0) и (4 ; 5). Скобки круглые, потому что знак неравенства строгий (крайние точки не включаются в ответ, т.к. в них функция как раз равна 3,5. А нам нужно больше).

3) Производная меньше нуля там, где функция убывает, а больше нуля там, где возрастает. Ищем промежутки возрастания\убывания функции. Там же будут решения исходных неравенств.

f’(x)<0 при x∈(-1,5 ; 2,5)
f’(x)>0 при x∈(-3,5 ; -1,5) и x∈(2,5 ; 5)

Скобки круглые потому что знак строгий. Запомните.

4) Найти такие точки не сложно. Ось абсцисс - горизонтальная ось. Проведя касательную к графику в точке x=-1,5 мы увидим, что она удовлетворяет условию.
Несколько сложнее обстоит дело с точкой х=2,5. В этой точке наблюдается излом графика. В математическом анализе доказывается, что в таких точках (излома) нельзя провести касательную вовсе. Поэтому для этой задачи ответ один: x=-1,5.

5) Значения функции смотрим по оси ординат. Наибольшее и наименьшее значения функции: ymin=-2; ymax=6.

Найти область определения функции: \(y=\sqrt{5x-3}\)

Область определения функции y=f(x) – это множество всех значений аргумента x, на котором задана функция.
Область определения функции f(x), как правило, обозначается как D(f).
При нахождении области определения функции y=f(x)= √(x^n) (корень n-ой степени) следует обращать внимание на четность или нечетность n. 
Подкоренное выражение для квадратного корня должно быть положительно:
5х - 3 ≥ 0
5x ≥ 3
x ≥ 3/5

Дана функция y = 3 cos x + 1. Найдите её область определения, множество значений и все значения x, при которых у = 1

Область определения - вся числовая ось. Множество значений : [-2, 4]. y=1 когда cosx=0. Это происходит при x= Pi/2 +nPi

Область определения   х∈(-∞;+∞)
Множество значений
Так как косинус - функция ограниченная, то
-1≤ cos x≤1
-3≤ 3cosx≤ 3
-3+1≤ 3 cosx +1 ≤3+1
-2≤3 cosx + 1 ≤4
E(y)=[-2;4]
y=1
Составляем уравнение
3cosx+1=1
3cos x=0
cosx=0
x=π/2 +  πk, k∈Z

Функция y=f(x) задана графиком. Укажите для этой функции: а) область определения; б)нули; в) промежутки знакопостоянства; г) промежутки возрастания(убывания); д) наибольшее и наименьшее значение функции; е) область изменения.

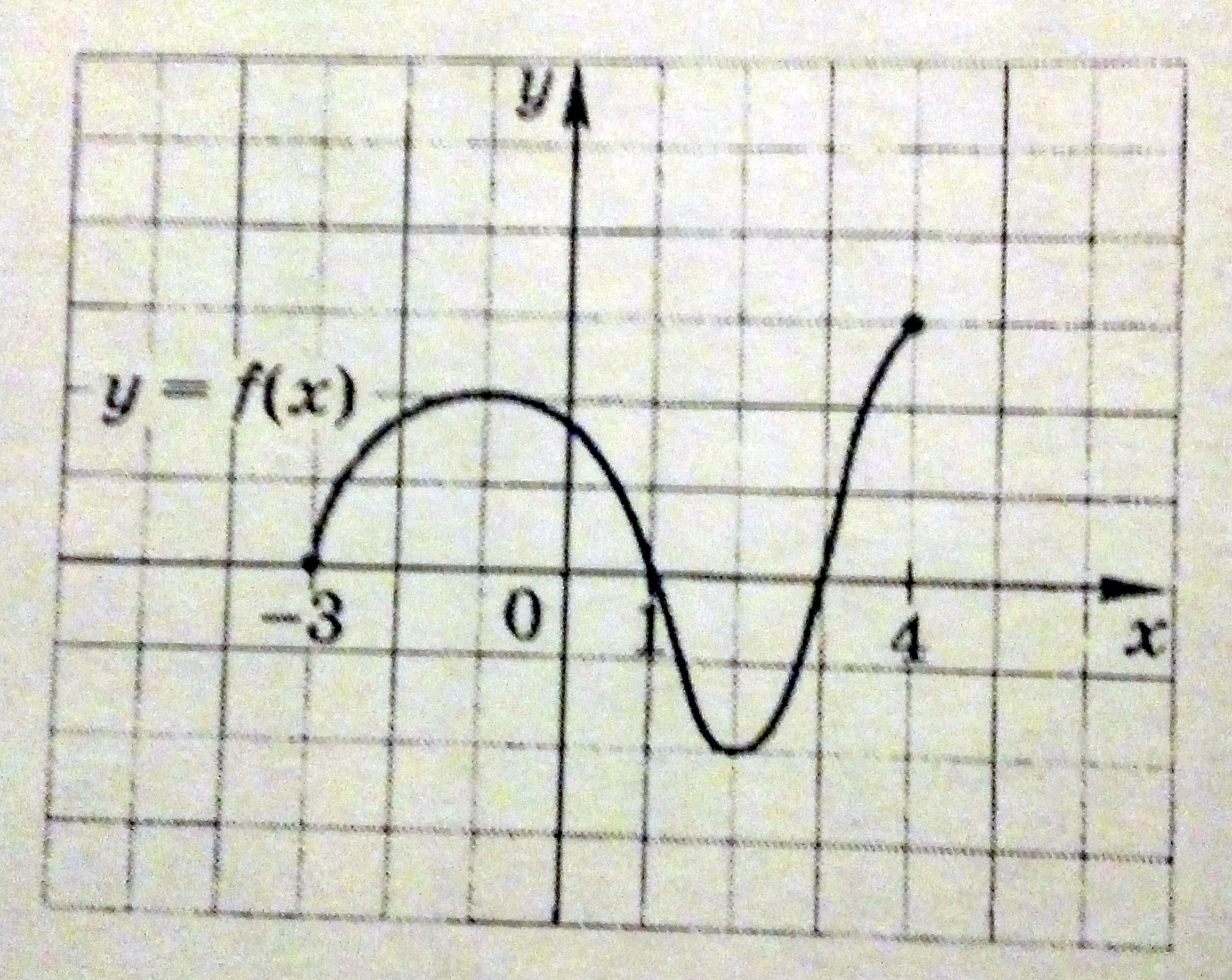
А) Область определения: x ∈ [-3; 4] (все значения x)
б) Нули: x = -3, x = 1, x = 3 (пересечения графика с осью OX)
в) Промежутки постоянства (график ниже или выше оси OX): 
y>0, при x ∈ (-3; 1) ∪ (3; 4]
y<0, при x ∈ (1; 3)
г) Возрастание и убывание:
y возр, при x ∈ (-3; -1) ∪ (2; 4)
y убыв, при x ∈ (-1; 2)
д) Наибольшее и наименьшее значение:
y наиб при x = 4. y наиб = 3
y наим при x = 2. y наим = -2
е) Область изменения (все значения y): [-2; 3]

Найдите область определения функции:
а) y=√x²-4+log3(5-x)
б) y=√9-1/x²

 y=√(x²-4) + log3(5-x)
Область определения:
x²-4 ≥ 0
5 - x > 0

x² ≥ 4
5 > x

x ≥ 2
x ≤ -2
x < 5

Область определения: (-∞; -2] ∪ [2;5)

y=√(9-1/x²)
Область определения:
9 - 1/x² ≥ 0
x² ≠ 0

1/x² ≤ 9
x ≠ 0

x^(-2) ≤ (1/3)^(-2)
x≠0

x ≥ 1/3
x ≤ -1/3
x≠0

Область определения: (-∞; -1/3] ∪ [1/3; +∞)