Найдите промежутки возрастания и убывания функции \(y=x^3+3x^2-9x\), точки экстремума

1) Функция определена на всей области R. Значит, она является непрерывной на всей области определения

2) Найдем производную данной функции
\( \displaystyle y`=3*x^2+6x-9 \)
Для того, чтобы найти точки экстремума данной функции нужно найти в каких точках производная равна нулю
\( \displaystyle 3x^2+6x-9=0 \)
разделим на 3
\( \displaystyle x^2+2x-3=0 \\ \displaystyle D=4-4*(-3)=4+12=16=4^2 \\ \displaystyle x_1= \frac{-2+4}{2}=1 \\ \displaystyle x_2= \frac{-2-4}{2}=-3 \)
Значит точки экстремума х=1 и х=-3

3) Чтобы определить какая из данных точек является точкой максимума, а какая точкой минимума необходимо рассмотреть значение производной на полученных интервалах

___+________-___________+_______
  -3 1

Если производная на промежутке принимает положительное значение то функция на данном промежутке возрастает, если отрицательное - то функция убывает

Значит на промежутке (-∞;-3) ∪ (1;+∞) функция возрастает
на промежутке (-3;1) убывает

4) если до точки х= -3 функция возрастает а после точки -3 убывает, значит при х= -3 точка максимума функции
 если до точки х=1 функция убывает, а после точки х=1 возрастает то в точка х=1 точка минимума

найдем значение функции в этих точках 

\( \displaystyle y(-3)=(-3)^3+3*(-3)^2-9*(-3)=-27+27+27=27 \\ \displaystyle y(1)=1^3+3*1^2-9*1=1+3-9=-5 \)

Функция задана формулой y = x²-4x-5 > 0. Используя ее график, определите промежуток, на котором функция убывает

Чтобы быстро ответить, надо на графике закрыть ту часть параболы, кторая идет вверх, и ответом будет оставшаяся открытой часть оси ОХ

---

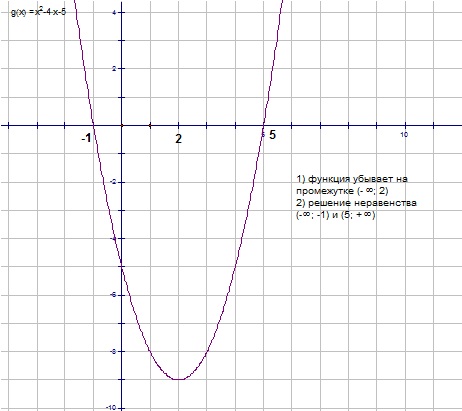
График y = x²-4x-5 представляет собой параболлу, ветви которой направлены вверх. Вешина параболлы смещена вниз и вправo и находится в точке (2,9).

Точки пересечения горизонтальной оси можно найти из уравнения  x²-4x-5=0

Найти интервалы возрастания, убывания функции \(f(x)=-3x^2-12x+50\)

Найти производную f' = -6x-12
приравнять к нулю  -6х-12=0, откуда х=-2
На оси отмечаем точку х=-2 и проверяем интервалы до -2 и после -2
Например, на интервале от минус бесконечности до -2 производная функции
f' > 0 (можно проверить, подставив  х=-4), значит сама функция на этом интервале  возрастает. Аналогично при х > -2  f' < 0 (проверяем подставив х=0)  значит при x > -2 функция убывает

F(x)=x³+2x²-4x-5 промежутки возрастания и убывания функции

F(x) возрастает когда первая производная положительна и убывает если производная отрецательная
F'(x)=(x³+2x²-4x-5)'=3x²+4x-4
определим промежутки знакопостоянства производной
f(x)=3x²+4x-4
Решим квадратное уравнение
х₁=-2
х₂=2/3
f(x)>0 (-∞;-2)∪(2/3;+∞)⇒F(x) возрастает на этих промежутках
f(x) < 0 (-2;2/3)⇒F(x) убывает на этом промежутке