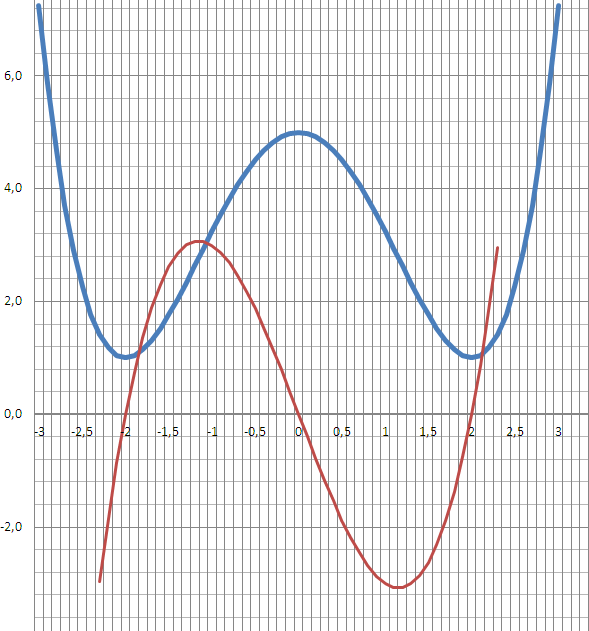
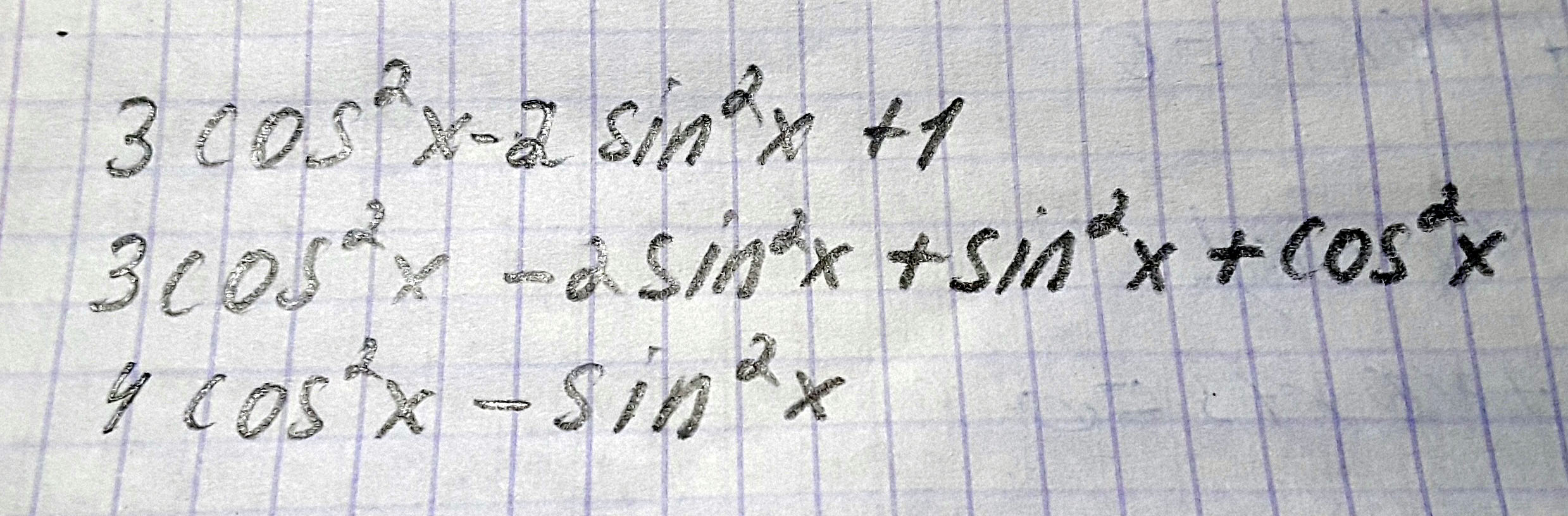Найдите наибольшее и наименьшее значение функции \(y=-x^3-3x^2+9x-2\) на отрезке [-2;2]

Для начала находим производную данной функции, \(y'=3x^2-6x+9\). Теперь приравниваем производную к нулю и находим точки, так как в данном уравнении дискриминант отрицательный и корней не существует, подставляем в первое уравнение границы и получаем точки максимума и минимума, т.е. \(y(-2)= (-2)^3-3(-2)^2+9(-2)-2=40\) это точка минимума, а точка максимума y = 8-3*4+9*2-2 = 12

План, по которому удобно находить наибольшее и наименьшее значение функции.

1. Если вам даны границы отрезка, то подставляете эти крайние значения в функцию вместо х и считаете.
2. Находите производную функции
3. Приравниваете ее к нулю
4. Решаете получившееся уравнение, находите корни (т.е. экстремумы функции)
5. Затем подставляете эти корни в ПЕРВОНАЧАЛЬНУЮ функцию (не в производную) и считаете
6. Из всех получившихся значений (и из границ отрезка тоже) выбираете нужное вам, т.е. наибольшее или наименьшее

Найдите наименьшее значение функции y = 10x - 5x^2 на отрезке [-1;2].

Для начала найдем производную:
f’(x)=10-10x
Теперь стационарные точки:
10-10х=0
10=10х
х=1.

Теперь смотрим, что нам надо найти - точки максимума(минимума) - это х или значения функции(это у). Второе.
Значит, подставляем конечные значения и стационарные точки в исходную функцию и смотрим, какое значение наименьшее.
Подставим -1:
10*(-1)-5*(-1)^2=-10-5=-15
Подставим 1:
10-5=5
Подставим 2:
10*2-5*4=20-20=0.

Наименьшее значение ФУНКЦИИ = -15.

Найдите наименьшее значение функции \(у=3(х-2)^2\) на отрезке -2,5

Нужно подметить, что при х=2 значение функции внезапно станет у=0.
А при любом другом х значение функции будет больше нуля, потому что в (х-2) квадрате, отрицательным не бывает.
Раз х=2 лежит внутри отрезка -2. 5, то вот и ответ:

Значение функции на отрезке -2. 5 минимально в точке х=2, и составляет у=0

Это минимальное значение верно не только на отрезке -2. 5, но и вообще во всей области определения функции, составляющей от минус бесконечности до плюс бесконечности.

Найти наибольшее и наименьшее значение функции \(у= -х^2+6х-1\)

1) вынесем минус за скобку:
y = -(x² - 6x + 1)
Выделим неполный квадрат:
y = -(x² - 6x + 9 - 8)
y = -(x² - 6x + 9) + 8
y = -(x - 3)² + 8
Графиком данной функции является парабола, ветви которой направлены вниз. Значит, наименьшего значения не будет.
Набиольлпе значение будет при х = 3 ((3 - 3)² = 0) и равно 8, т.к. Наименьшее значение у будет при том значении х, при котором квадратная скобка является наибольшей, т.к. Она со знаком минус.

2) Найдём xв
хв = -6/(-2) = 3
yнаим = -9 + 18 -1 = 8

Ответ: 8.

Найдите наибольшее значение функции f(x)=3cos²x-2sin²+1

Легко увидеть, что два слагаемых полученного выражения принимают положительное значение, причем чтобы выражение было максимальным, нужно, чтобы косинус квадрат икс был макс и синус квадрат икс был минимальным, а зная, что когда косинус равен единице, синус равен нулю, то получается, что максимальное значение будет в точках, где косинус принимает знач 1, соответсв макс знач равно 4.
это можно проверить взяв производную от этого выражения и приравняв ее к 0.

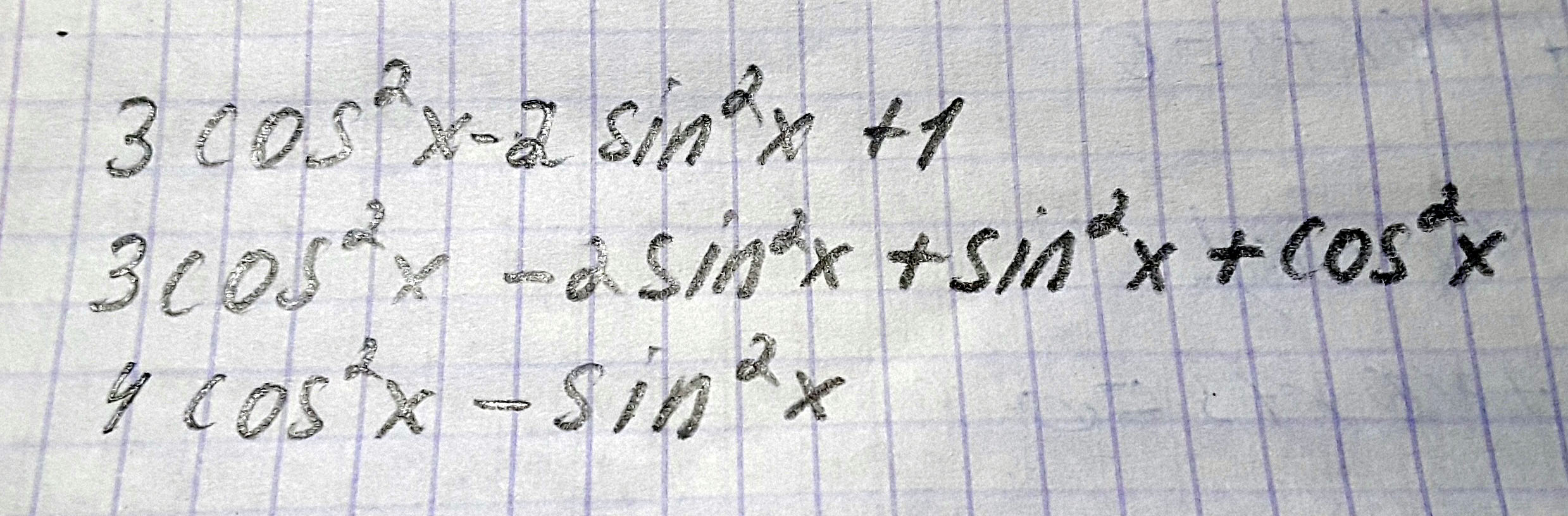
Найти наибольшее значение функции \(у=-х^2+10х-3\) на отрезке [1;8]

Сперва найдем критические точки, найдя производную, приравняв ее к 0 и найдя корни
\( y’=-2x+10 \)
\( -2x+10=0;x=5 \)
5 входит в исходный отрезок, тогда найдем значения функции в х=5 и на границах отрезка
\( y(1)=-1+10-3=6 \)
\( y(5)=-25+50-3=22 \)
\( y(8)=-64+80-3=13 \)
наибольшее - y(5)=22

У=-х²+10х-3
у’=-2х+10=0
2х=10
х=5

у(1)=-1²+10*1-3=-1+10-3=6 наим
у(5)=-5²+10*5-3=-25+50-3=22 наиб
у(8)=-8²+10*8-3=-64+80-3=13

1) Определите наибольшее значение функции \(f(x)=\sqrt{9-х^2}\)
2) Сколько точек пересечения имеют графики функций у=6 и \(у=|х^2-6х+5|\)
3) Найдите наименьшее значение функции \(у=х^6+3\)

1) Найдём область определения этой функции: 9 - х² ≥ 0, получаем  отрезок -3; 3, т. Е  -3 ≤ х ≤ 3
 Найдём производную данной сложной функции, она равна
1 ÷ 2√9 - x²  умноженное на производную от аргумента, т.е. на производную от ( 9 - x² )
Получаем 1 ÷ 2√ 9 - x² × (-2x) = - x ÷ √ 9 - x²
Найдём критические точки функции. Производная равна нулю 
при  х = 0, значение функции в этой точке равно 3
рассмотрим значения функции на концах отрезка, т.е. При х =-3 и х = 3, они равны нулю. Значит, наибольшее значение функция принимает при х = 0 и оно равно 3.

2) у = 6 и у = |x² - 6x + 5|

Построим сначала график функции у = х² - 6х + 5
Нули функции х = 1 и х = 5
Координаты вершины  х = ( 1 + 5 )÷ 2, х = 3, у = -4
для построения графика возьмём ещё одну точку, пусть х = 0, тогда у = 5
Через вершину параболы проходит ось симметрии. Отразим полученную точку симметрично полученной точки с координатами (0;5) и по пяти полученным точкам построим график.
Чтобы построить график функции у = |x² - 6x + 5|, отобразим нижнюю часть графика симметрично относительно оси абсцисс.
График функции у = 6 - это прямая линия, параллельная оси абсцисс и проходящая через точку ( 0; 6 )
Два графика данных функций имеют две точки пересечения.

3) Найдём наименьшее значение функции \(у = х^6 +3\) 
Функция определена для любого х
Найдём производную этой функции, она равна \(6х^5\)
Производная равна 0 при х = 0
Рассмотрим знак производной на интервалах, определённых этой критической точкой:
при х ⊂ ( -∞; 0] производная имеет знак минус,
при х ⊂ [ 0; +∞) производная имеет знак плюс.
Значит, на первом интервале функция убывает, а на втором возрастает
у ( 0 ) = 3. Это и есть наименьшее значение функции.

Найти точки максимума функции у=1/4х^4-2x^2+5

Точки экстремума - производная равна =
Y’ = x³ - 4*x = 0 или  х*(х²-4)=0 или корни х1= 0 х2= -2  и х3=+2
Остается сосчитать значения  -  для Х = 0
Ymax = Y(0) = 5 - максимум
Дополнительно - график
При х= +/-2 - минимумы