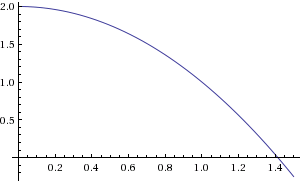
Вычислить площадь фигуры, заключенной между графиками функций Y=2√(X) и Y=X Сделать чертеж.

Площадь фигуры, которую необходимо вычислить, изображена на рисунке. Найдем точки пересечения графиков:

\( 2\sqrt{x}=x \)

\( 4x=x^2 \)

\( 4x-x^2=0 \)

\( x=0 \)

\( x=4 \)

Вычислим площадь фигуры, применяя определенный интеграл:

\( \int\limits^4_0 {f(x_1)-f(x_2)} \, dx =\int\limits^4_0 {x-2\sqrt{x}} \, dx =(\frac{x^2}{2}-\frac23x^{\frac{3}{2}})|_0^4=\frac{4^2}{2}-\frac23*2^3=8-\frac{16}{3}=\frac{8}{3} \)

Ответ: площадь равна \( \frac{8}{3} \) квадратных единиц

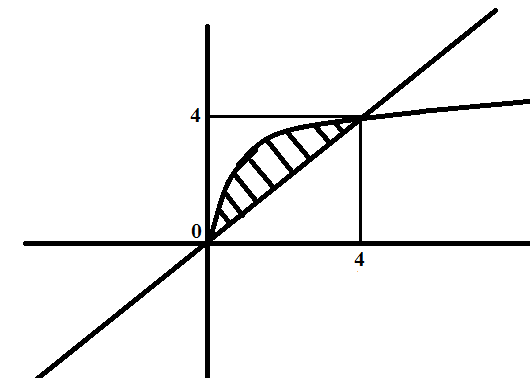
Вычислите площадь фигуры, ограниченной графиками функций: \(y=1-x^2\), y=-x-1.

\( S_{fig}=\int\limits^2_{-1} {1-x^2+x+1} \, dx=\int\limits^2_{-1} {2-x^2+x} \, dx=2x-\frac{x^3}{3}+\frac{x^2}{2}|^2_{-1}=\\=4-\frac{8}{3}+2+2-\frac{1}{3}-\frac{1}{2}=4.5 \)
Вот график и область фигуры:

Парабола пересекается с прямой в точках -1 и 2. Она находится выше прямой, значит вычитаем из неё прямую

S = \( \int\limits^2_{-1} {((1 - x^2) - (-x - 1))} \, dx = 2x - \frac{x^3}{3} + \frac{x^2}{2}|_{-1}^2 =\\= (2*2 - \frac{2^3}{3} + \frac{2^2}{2}) - (2*(-1) - \frac{(-1)^3}{3} + \frac{(-1)^2}{2} = 4.5 \)

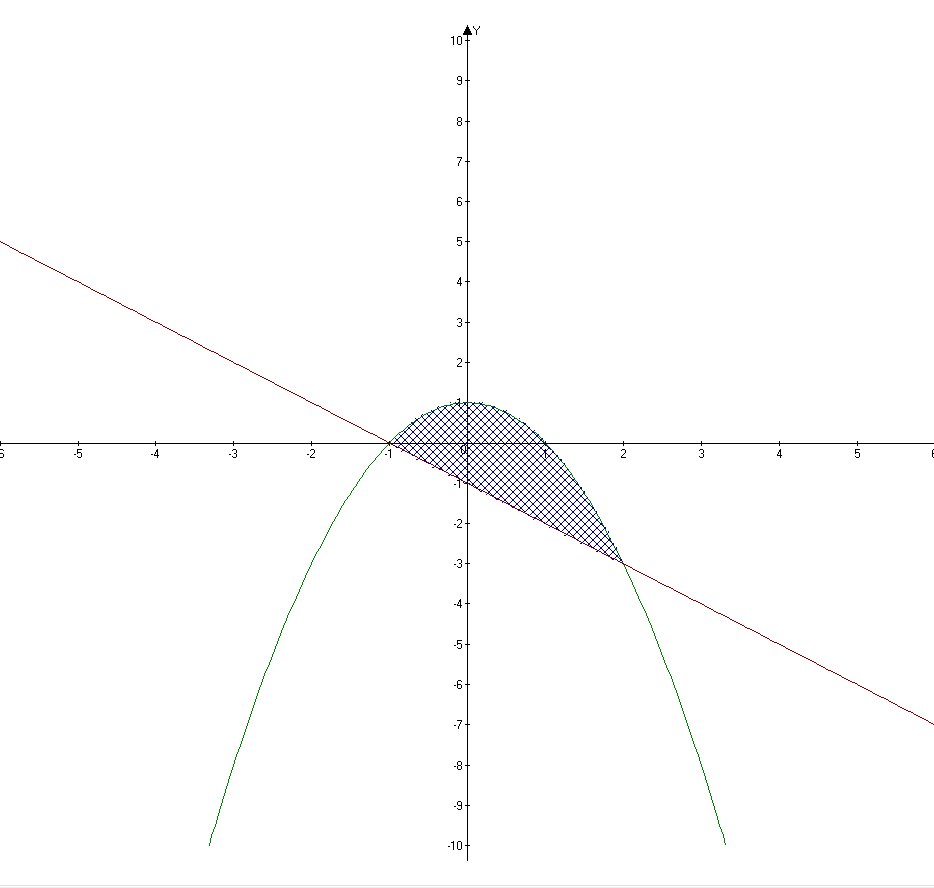
Вычислить площадь фигуры, ограниченной графиком функции \(у=1-х^2\) и осью Ох.

Найдем координаты  пересечения  параболы  с осью 0 ОΧ  на этой оси все y=0

потому  1- x² = 0; x²= 1;   x=(-1 )   или    x=  1

площадь  этой фигуры   ест  интегралом   функции   w  отрезке [ -1, 1]

INT ( 1- x² )  dx =  x- x³/3  + C

Площадь =  ΙΝΤ f(x)  "где x=1"    -   ΙΝΤ f(x)  "где x=-1"  = [(1-1/3)] - [( (-1) - (-1)/3)] = 4/3

Треугольник образован осями координат и касательной к графику функции \(y=2x^2-3x-5\) в точке \(x_0=2\). Площадь этого треугольника
1. 16,9 ед^2
2. 19 ед^2
3. 19,5 ед^2?

Касательная к графику y = 2x^2 - 3x - 5 в точке x0 = 2
f(x) = y(x0) + y ’ (x0)*(x - x0)

1) Найдем производную
y ’ (x) = 4x - 3
y ’ (x0) = f ’ (2) = 4*2 - 3 = 5

2) y(x0) = y(2) = 2*2^2 - 3*2 - 5 = 8 - 6 - 5 = -3

3) Касательная
f(x) = -3 + 5(x - 2) = -3 + 5x - 10 = 5x - 13

4) Найдем точки пересечения касательной с осями координат
x = 0: f(0) = -13;
f(x) = 0: 5x - 13 = 0; x = 13/5

5) Этот треугольник - прямоугольный с катетами 13 и 13/5.
Его площадь равна половине произведения катетов.
S = 1/2*13*13/5 = 169/10 = 16,9
Ответ: 1. 16,9

Вычислите площадь фигуры, которая ограничена графиком функции \(y=x^2-x-6\) и осью абсцисс

Можно сразу сказать, что график - парабола, с ветвями, направленными вверх. (Смещенная вниз на 6 единиц)
Площадь заштрихованной фигуры и надо найти.
Такое считается при помощи интеграла. Т.е. площадь фигуры, ограниченной графиком функции y(x) осью абцисс и в общем случае прямыми x=a и x=b (криволинейной трапеции) равна:
\( S= \int\limits^a_b {y(x)} \, dx \)  (1)
Где пределы интегрирования a,b нам надо определить. В нашем случае это x-координаты точек пересечения графика с осью абцисс, т.е. корни уравнения:
\( y(x)=0 \)
\( x^2-x-6=0 \)
Решаем его (квадратное уравнение)
D=1+4*1*6=25
x₁=-2;  x₂=3
Далее, подставляем в формулу площади (1) нашу функцию и пределы интегрирования
Так, площадь получилась отрицательной. Ну и правильно, у нас фигура под осью x лежит. Такое может получиться и при вычислении мощности переменного тока на части периода, например. Там знак важен.
А поскольку нам надо площадь, можно записать модуль результата: \( S= 20\frac{5}{6} \)

Изобразить криволинейную трапецию, ограниченную графиком функции \(y=2-x^2\), y=0 прямыми x=0

Запишем уравнение по-другому
\( y=- x^{2} +2 \)
начертим график \( y= x^{2} \)
начертим симметрично оси Ох. Сместим на 2 ед. вверх. Ограничим осями Ох и Оу.