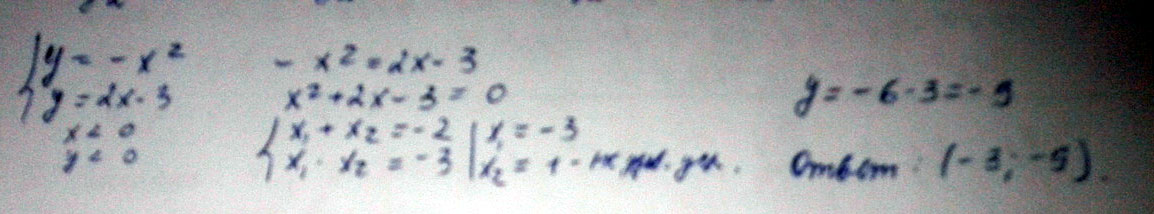Определите коэффициенты к и в функции у=kx+b, если известно, что график данной функции проходит через точку М(2;1), параллельно прямой y=3x-1. Найдите координаты точек пересечения функции с осями координат
1)Так как график проходит через точку М(2;1), то ее координаты удовлетворяют уравнению функции. Подставим х=2 и у=1 в уравнение у=kx+b, получим 2k+b=1.
2) Так как шрафики параллельны ( а это прямые по условию задачи), то их угловые коэффициенты равны, значит k=3.
3) Подставим k=3 в уравнение 2k+b=1, 2·3 + b=1, b=-5.
Значит, график искомой функции задается уравнением у=3х-5.
4) Найдем точки пересечения графика функции у=3х-5 с осями координат.
С осью ОУ: х=0, значит у=-5. А(0;-5)
С осью ОХ: у=0, значит 0=3х-5, х=5/3 или х=1⅔. В( 1⅔ ;0).
(Данных достаточно для построения прямой, постройте самостоятельно).
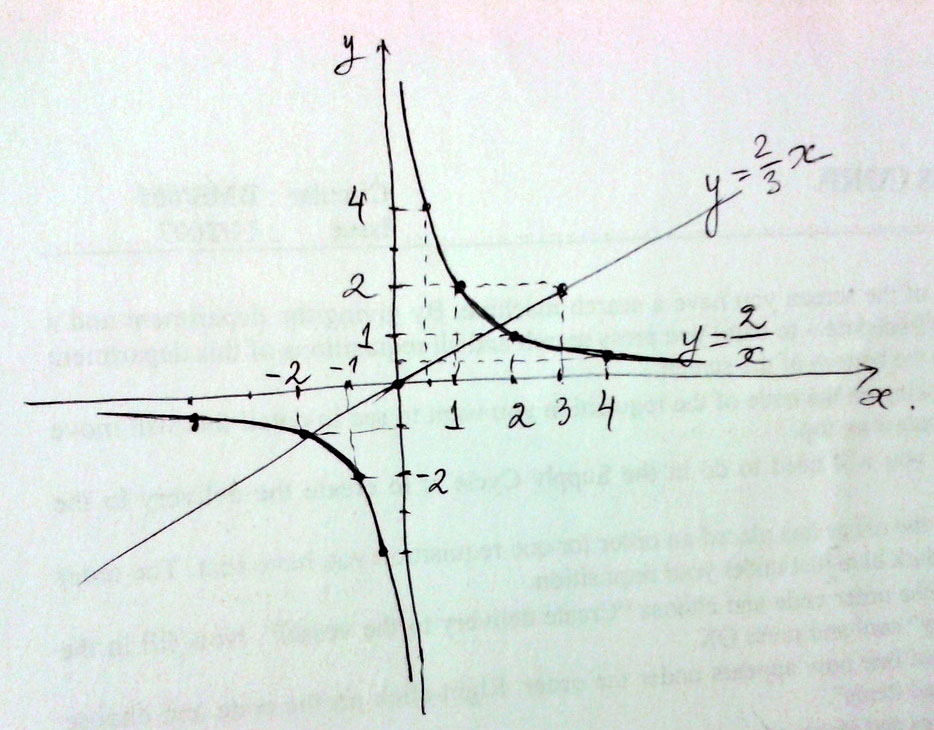
Постройте на одной и той же координатной плоскости графики функций y=2/x и y=[2/3]*x
Найдите координаты точек пересечения графиков. Определите, являются ли данные функции возрастающими или убывающими. Определите, при каких значениях аргумента обе функции будут принимать положительные значения.
У=2/х - это гипербола
у=2х/3 - это прямая
Точки пересечения:\(\frac{2}{x}=\frac{2}{3}x, \frac{2}{x}=\frac{2x}{3}, \to{x^2=3} \\x=\pm{\sqrt{3}} \to{y=\pm{\frac{2}{\sqrt{3}}}} \\ (\sqrt{3},\frac{2}{\sqrt{3}}), (-\sqrt{3},\frac{2}{\sqrt{3}})\).
Функция у=2х/3 возрастающая на всей области определения, на (-беск. +беск. ).
Функция у=2/х убывающая в обл. опред. на участке (-беск,0) и на (0,+беск).
Обе ф-ции принимают положительные значения при х > 0.
Не выполняя построения, установите взаимное расположение графиков линейных функций. В случае пересечения графиков вычислите координаты точки пересечения.
а) у = 2х и у = 2х – 4;
б) у = х + 3 и у = 2х – 1;
в) у = 0,5х + 8 и у =21х + 8
г) у = 2х – 2 и у = -0,5х + 3
Линейной функцией называется функция вида y=kx+b
а) у = 2х и у = 2х – 4 - графики параллельны, поскольку их угловые коэффициенты (k) равны, следовательно, они не пересекаются и не имеют общих точек.
б) у = х + 3 и у = 2х – 1 - графики пересекаются, поскольку их угловые коэффициенты различны.
Найдем точку пересечения, приравняв правые части:
х + 3 = 2х – 1
x=4, y=4+3=7.
Координаты точки пересечения - (4;7).
в) у = 0,5х + 8 и у =21х + 8 - графики пересекаются, поскольку их угловые коэффициенты различны.
Поскольку и в первом, и во втором случае b=8, то точка пересечения графиков - (0,b) - (0;8).
г) у = 2х – 2 и у = -0,5х + 3 - графики пересекаются, поскольку их угловые коэффициенты различны.
Найдем точку пересечения, приравняв правые части:
2х – 2 = -0,5х + 3
2,5x=5
x=2, y=2*2-2=2.
Координаты точки пересечения - (2;2).
А) Функции будут параллельны по отношении друг к другу. Причем, вторая функция 2x-4 ниже графика 2x
б) В этом случае графики имеют одну общую точку, поскольку эти две функции задаются прямыми, и их коэффициенты пропорциональности НЕ равны. Давайте проверим, какую общую точку они будут иметь:
\( x+3=2x-1 \\ x=4 \)
Подставив x в любое из функций, получим, что y=7.
Т. Е общая точка - это M(4;7)
в) Эти функции равны. Они имеют бесконечно много общих точек.
г) Найдем общую точку:
\( 2x-2=-0,5x+3 \\ 2,5x=5 \\ x=2 \)
Общая точка - это точка M(2;2).
Прямые имеют только одну общую точку, значит, графики пересекаются только в ОДНОЙ точке.
Найдите координаты точки пересечения графиков функций \(y = -x^2\) и y = 2х-3, лежащей в третьей координатной четверти
- X^2 = 2X - 3
X^2 + 2X - 3 = 0
D = 4 + 12 = 16 ; √ D = 4
X1 = ( - 2 + 4 ) : 2 = 1
X2 = ( - 6 ) : 2 = ( - 3 )
Y = 2X - 3
Y1 = 2 - 3 = ( - 1 )
Y2 = - 6 - 3 = - 9
Точки пересечения графиков ( 1 ; - 1 ) и ( - 3 ; - 9 )
В 3-ей координатной точки лежит точка ( - 3 ; - 9 )
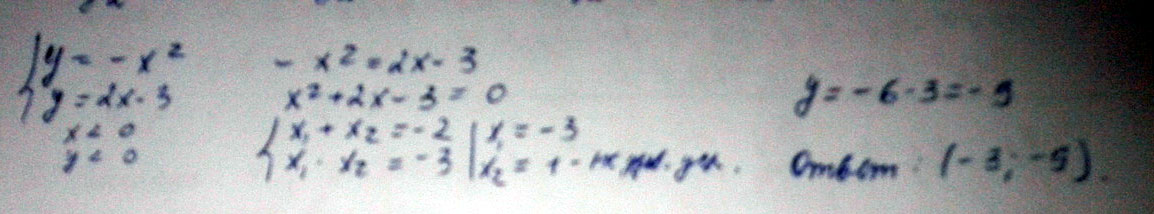
у=7х+63
1) построить график
2) при каких "х" у=0, у > 0, у < 0
3) при каких х функция возрастает, убывает
4) найти координаты точек пересечения данного графика с функцией.
У=7х+63,
Чертим систему координат.
график прямая, строим по двум точкам (ед отрезок 1 клетка 9 ед):
х= 0 -9
у= 63 0
ставим первую точку по х не двигаемся, по у 7 клеток вверх
ставим вторую точку по х 1 клетка влево, по у никуда не двигаемся.
Соединяем две точки, подписываем график функции.
у=0 х=-9
y>0 при х∈(-9; + бесконечность)
у<0 при х∈(- бесконечность; -9)
функция возрастает на всей области определения х∈(-беск, + беск) или х∈R
функция пересекает ось абсцисс в точке (-9;0)
функция пересекает ось ординат в точке (0;63)
Прямая у = - 6х - 2 является касательной к графику функции \(у = х^3 - 5x^2 + x - 5\). Найдите абсциссу точки касания
Найдем производные и приравняем.
у1' = -6 и \(y2' = 3x^2 -10x + 1\)(угловой коэффициент прямой равен тангенсу угла наклона касательной).
\(3х^2-10х+1 = - 6 \\ 3х^2 - 10х + 7 = 0 \\ D=100-84=16 \\ x_1=1; x_2=\frac{7}{3}\). Кроме того, у1(1) = -6-2= - 8
у2(1) = 1-5+1-5 = - 8, т.о. точка (1;-8) - точка касания.
Проверим у1(7/3) и у2(7/3). Равенства не получим, это значит, что касательная ко второму графику будет параллельна прямой у1, но не сливаться с ней.Ответ: 1.
К графику функции \(f(x)=3+7x-4x^2\) проведена касательная, с угловым коэффициентом, равным -9. Найдите координаты точки касания
Производная функции в заданной точке равна тангенсу угла наклона касательной к графику функции в этой точке.
Производная равна -8х + 7 = -9
-8х = -16
х = -16/-8 = 2.
Подставим это значение в уравнение \(f(x)=3+7x-4x^2\) и находим координату по оси у:
у = 3 + 7*2 - 4*2² = 3 + 14 - 16 = 17 - 16 = 1
Ответ: (2; 1)
На графиках функции y=x^2+6x-33 и y=-x^2+5x-3 найдите точки A(x1;y1) и B(x2;y2) так, чтобы координаты вектора AB были {-3;8}
Координаты точки А(к; к²+6к-33).
Координаты точки В(п;-п²+5п-3).
Пишем координаты вектора АВ{п-к;(-п²+5п-3)-(к²+6к-33)}
Составляем систему уравнений:
п-к=-3;
-п²+5п-3-к²-6к+33=8
Решаем способом подстановки : п=к-3
-(к-3)²+5(к-3)-3-к²-6к+33-8=0
-2к²+5к-2=0; D = 9: k=0.5; k = 2
n=-2.5 ; n=-1
Первое решение A(0.5; 0.5²+6*0.5-33)⇔(0.5;-29.75)
B(-2.5;-(-2.5)²+5*(-2.5)-3)⇔(-2.5;-21075).
Второе решение А(2;2²+6*2-33)⇔(2;-17)
В(-1; -(-1)²+5*(-1)-3)⇔(-1;-9)
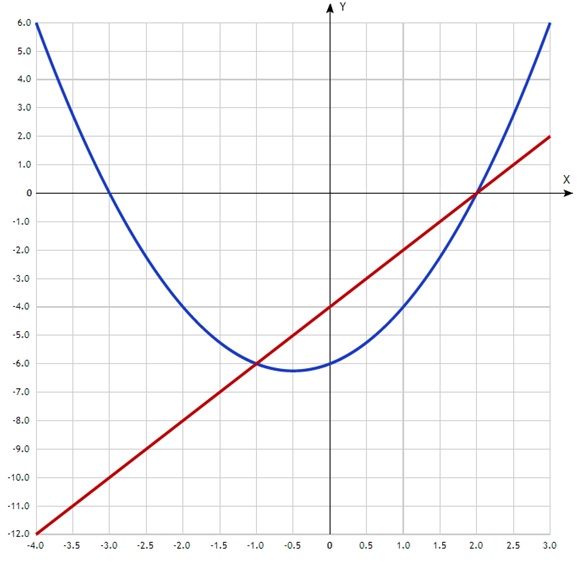
Постройте график функции y=x^2+x-6
а)найдите по графику функции промежутки, в которых y>0 и y<0
б)не выполняя дополнительных построений, найдите координаты точек пересечения данного графика с графиком функции y=2x-4
График функции y=x^2+x-6 это парабола ветвями вверх.
а)найдите по графику функции промежутки, в которых y>0 и y<0.
Для этого надо определить точки на оси ОХ, в которых график эту ось пересекает.
Приравниваем квадратный трёхчлен нулю.
x²+x-6 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=1²-4*1*(-6)=1-4*(-6)=1-(-4*6)=1-(-24)=1+24=25; Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√25-1)/(2*1)=(5-1)/2=4/2=2; x₂=(-√25-1)/(2*1)=(-5-1)/2=-6/2=-3.
На промежутке (-3;2) график проходит ниже оси ОХ - там значения у отрицательные.
На промежутках (-∞;-3) и (2;+∞) значения у положительные.
б)не выполняя дополнительных построений, найдите координаты точек пересечения данного графика с графиком функции y=2x-4.
Для этого надо приравнять функции:
x²+x-6 = 2х-4.
Получаем квадратный уравнение:
х²-х-2 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-1)^2-4*1*(-2)=1-4*(-2)=1-(-4*2)=1-(-8)=1+8=9; Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√9-(-1))/(2*1)=(3-(-1))/2=(3+1)/2=4/2=2; у = 2*2-4 = 0;x₂=(-√9-(-1))/(2*1)=(-3-(-1))/2=(-3+1)/2=-2/2=-1. у = 2*(-1)-4 = -6.
Получили 2 точки: (2;0) и (-1;-6).
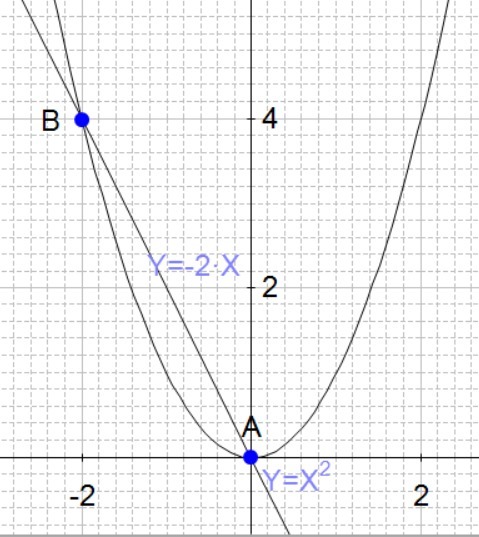
Постройте графики функций y=x² и y=-2x. Найдите координаты точек их пересечения
X²=-2x x²+2x=0 x(x+2)=0 x=0 или х=-2 тогда у=0 или у=4
ответ: (0;0), (-2;4)
Графики функций y = x² и y = -2x на рисунке пересекаются в точках A и B.