Постройте график функции и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку

Используем теорему Виетта. По ней полином в числителе имеет два корня, если заменить \(z=x^2 \\ z_1 =  4, \;\;z_2 = 9\)
Проверяем 9+4 = 13 = -p, z1*z2 = 36 = q

Подставляя x1,2 = sqrt(4), получим два корня исходного уравнения: x1 = 2, x2 = -2,

точно также x3= 3, x4 = -3.
Значит полином в числителе разлагается на множители:

(x-2)(x+2)(x-3)(x+3). Что-то можно сократить, после сокращения дроби останется y=(x+3)(x-2). Сразу же ясно, что это парабола, и пересекает ось абцисс в точках x=-3 и x = 2, значения y в обоих этих точках, очевидно ноль. Вершина параболы находится посередине между этими точками, то есть x=-0.5. Значение функции в этой точке y=(3-0.5)(-0.5-2)=-6.25.

Вторая часть вопроса говорит о прямой y=m. Очевидно, что эта прямая параллельна оси абцисс, и будет иметь общую одну точку только в вершине параболы, которую только что нашли, то есть m = -6.25

На графике изображены парабола и прямая y=-6.25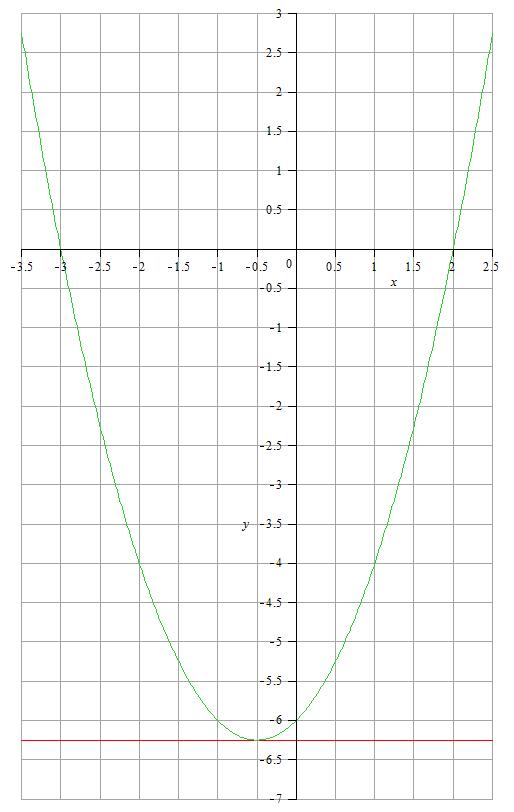 

Найдите все значения К, при каждом из которых прямая у=кх имеет с графиком функции у=х^2+4 ровно одну общую точку

x^2+4=kx условие общей точки

x^2-kx+4=0

Чтобы данное уравнение имело одно решение D=0

D=k^2-16=0

k1=4

k2=-4

просто приравниваете

k*x = x^2 + 4; 

x^2 - k*x + 4 = 0;

Если это квадратное уравнение имеет ровно один корень, то это как раз то что надо.

А один корень тогда, когда это полный квадрат. То есть к = 4 или -4. 

В самом деле, это можно и так записать:

(x - k/2)^2 = k^2/4 - 4; и полный квадрат получается, если правая часть равна нулю, то есть k^2 = 16; 

Например, прямая y = 4*x в точке x= 2 равна 8, и x^2 + 4 = 8; больше нет общих точек. То же самое y = -4*x в точке x= -2 равна 8, и x^2 + 4 = 8;

Найдите все значения к, при каждом из которых прямая у=кх имеет с графиком функции \(у=x^2+4 \) ровно одну общую точку. Постройте этот график и все такие прямые.

Приравниваем два уравнения графиков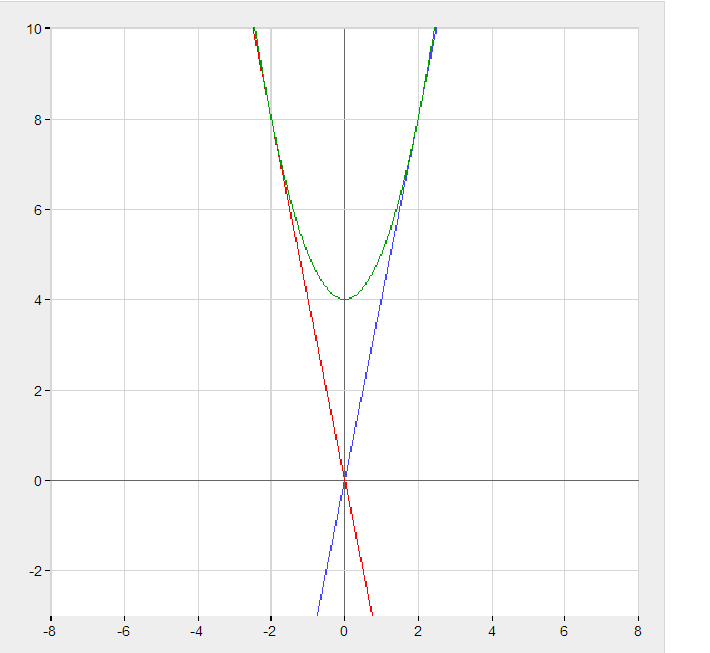
\( kx=x^2+4 \)
\( x^2-kx+4=0 \)
имеет одну точку, если дискеменант равен нулю
\( D=k^2-16 \)
\( k^2-16=0 \)
\( k=\pm 4 \)

сам график нарисован зеленым цветом (y=x^2+4),
прямые - красным (y=-4x) и синим (y=4x)

Постройте график функции y=x²-|x|+2 и определите, при каких значениях параметра a прямая y=a имеет с графиком ровно две общие точки

Раскройте по-разному выражение внутри модуля и постройте два графика в зависимости от ограничений. Получится следующая картинка. Точки вершины x=1/2 (-1/2) y=7/4. Ровно 2 общие точки будут при а=7/4 и а (2; беск. ). P.S. y=a - горизонтальная прямая.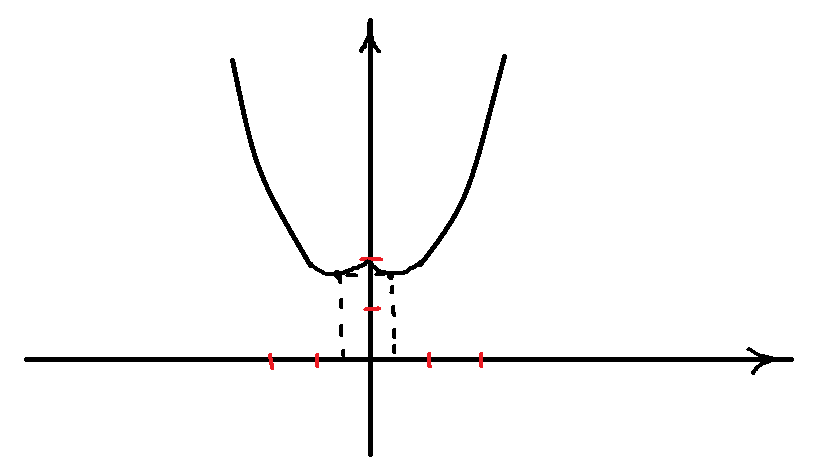

Постройте график функции \(y=-x^2+|x|+4\) и определите, при каких значениях параметра (a) прямая y=a имеет с графиком ровно две общие точки

При x < 0 будет ветка параболы y = -x^2 - x + 4
y(0) = 4, y(-1) = -1 + 1 + 4 = 4, y(-2) = -4 + 2 + 4 = 2, y(-3) = -9 + 3 + 4 = -2
Значит, при x = -0,5 у нее максимум y(-0,5) = -0,25 + 0,5 + 4 = 4,25
А примерно при x от -2,6 до -2,5 график пересечет ось Ox:
y(-2,5) = -6,25 + 2,5 + 4 = 0,25; y(-2,6) = -6,76 + 2,6 + 4 = -0,16
При x > 0 будет ветка параболы y = -x^2 + x + 4
y(0) = 4, y(1) = -1 + 1 + 4 = 4, y(2) = -4 + 2 + 4 = 2, y(3) = -9 + 3 + 4 = -2
Значит, при x = 0,5 у нее максимум y(0,5) = -0,25 + 0,5 + 4 = 4,25
А примерно при x от 2,5 до 2,6 график пересечет ось Ox: 
y(2,5) = -6,25 + 2,5 + 4 = 0,25; y(2,6) = -6,76 + 2,6 + 4 = -0,16
Этого достаточно, чтобы самостоятельно построить график.
Прямая y = a имеет с графиком 2 общие точки при a = 4,25 и при a < 0

Постройте график функции \(y=\frac{x^4-5x^2+4}{(x+1)(x-2)}\) и определите, при каких значениях c прямая y=с имеет с графиком функции только одну общую точку

Числитель - это биквадратный многочлен. Его можно разложить на множители: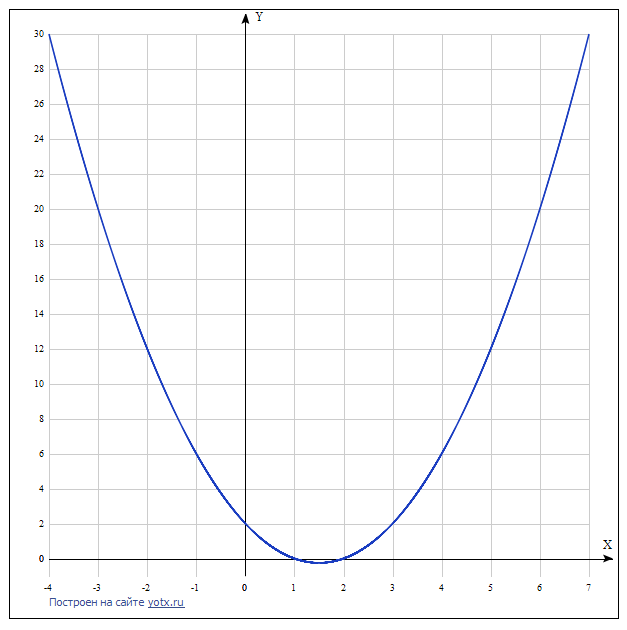
Заменим х² = у.
Получаем квадратный трёхчлен: у² - 5у + 4. Приравняем его нулю.
у² - 5у + 4 = 0.
Квадратное уравнение, решаем относительно y: 
Ищем дискриминант:D=(-5)^2-4*1*4=25-4*4=25-16=9;
Дискриминант больше 0, уравнение имеет 2 корня:
y_1=(2root9-(-5))/(2*1)=(3-(-5))/2=(3+5)/2=8/2=4;
y_2=(-2root9-(-5))/(2*1)=(-3-(-5))/2=(-3+5)/2=2/2=1.
Отсюда х = +-2   и х = +-1.
Числитель приобретает вид (х+1)(х-1)(х+2)(х-2).
После сокращения у = (х-1)(х-2).
Это даёт 2 корня: х = 1  и х = 2.
График - парабола у = х² - 3х + 2.
Осталось найти касательную, проходящую через начало координат.
Примерно, это у = -5,8х.

Построить график функции
y = |x|x-|x|-3x
При каких значениях m прямая y=m имеет с графиком ровно две общие точки

Две общие точки прямая y=m имеет, как видно из графика лишь при двух значениях параметра m :  -4 и 1. Для иллюстрации эти два варианта прямой y=m показаны красным. При любых остальных значениях будут либо 1, либо 3 точки пересечения.