Принадлежат ли точки графику функции


Главная Научный калькулятор
Меню Алгебра Геометрия Основные понятия Аксиомы планиметрии Углы Перпендикулярные и параллельные прямые Перпендикуляр и наклонная Круг (окружность) Треугольник Четырехугольник Параллелограмм Трапеция Многоугольники Основные понятия стереометрии Аксиомы стереометрии Прямые в пространстве Пересекающиеся прямые Параллельные прямые Скрещивающиеся прямые Прямая и плоскость в пространстве Перпендикулярность прямой и плоскости Параллельность прямой и плоскости Угол между прямой и плоскостью Теорема о трех перпендикулярах Формула двойного проектирования Плоскости в пространстве Пересекающиеся плоскости Параллельность плоскостей Перпендикулярность плоскостей Площадь проекции плоской фигуры на плоскость Многогранники: Пирамида Призма Тела вращения: Цилиндр Конус Шар (Сфера) Объем тел вращения Задачи по геометрии Примеры решений Вспомогательные материалы: Таблицы Брадиса Исследование функций Асимптоты. Первая производная. Вторая производная. Графики функций Задачи по функциям Тригонометрия Тригонометрические неравенства	Постройте график функции у=-х+3. Принадлежит ли графику точка А(-13; 16)? У= -х+3 график - прямая, для построения достаточно двух точек х= 0 3 у= 3 0 Чертим систему координат, отмечаем положительное направление вверх и вправо; ед отрезок выбираем в одну клетку. Отмечаем точки (0;3) (3;0) Чертим прямую, проходящую через эти точки. Проверяем точку А(-13;16), подставляем её координаты вместо х и у в уравнение прямой у=-х+3, получаем: 16=13+3 16=16 верно, значит точка А принадлежит прямой. Постройте график функции y=4-2x. 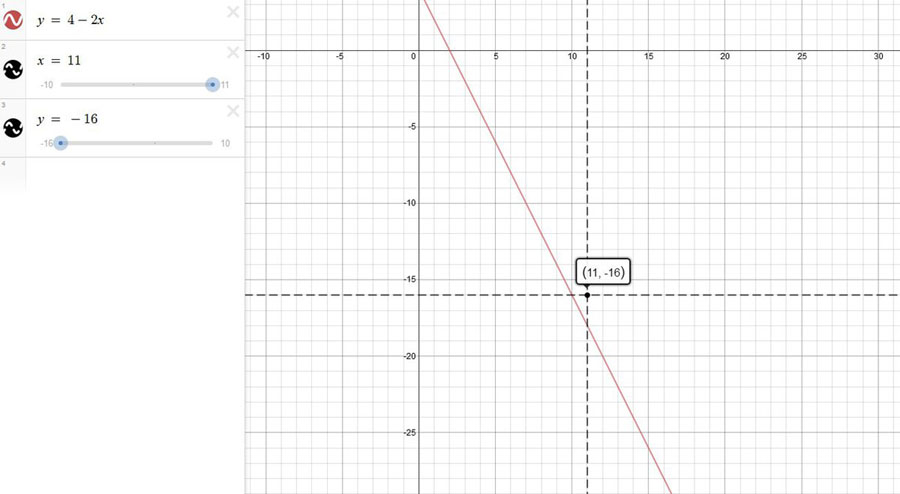Выясните, принадлежит ли графику точка M(11;-16) Смотрите рисунок. Построим график функции \( y = 4-2x \) (на рисунке красным цветом). Отметим точку с координатами \( x = 11 \), y = \( -16 \) (на рисунке точка получается на пересечении двух пунктирных линий). Проверим, «лежит» ли она на графике нашей функции или нет. Как видим, точка не принадлежит графику функции. Принадлежат ли графику функции y = -7x следующие точки: a (0;-1); b (-1;7); c (2;-14); d (-3;21)? А (0;-1)⇒х=0, у=-1. Теперь подставляем в уравнение: -1=0. (это неверно) значит точка не принадлежит графику. В (-1;7)⇒х=-1, у=7, подставляем в уравнение: 7=7. (это верно) точка принадлежит графику. С (2;-14)⇒ х=2, у=-14, подставляем: -14=-14, (это верно) точка принадлежит графику. D (-3;21)⇒ х=-3, у=21, подставляем: 21=21 (это верно) точка принадлежит графику. Одна из следующих точек принадлежат графику функции y=3x² A(0,0); B(1;1); C(1;2); D(-1;2); E(3;-9); F(4;-2); K(2;-4) \( y=3x^2 \) \( 30^2=0 \) A(0,0) принадлежит гарфику \( 31^2=3 \neq 1; \) B(1;1) не принадлежит гарфику \( 31^2=3 \neq 2; \) C(1;2) не принадлежит гарфику \( 3(-1)^2=3 \neq 2; \) D(-1;2) не принадлежит гарфику \( 33^2=27 \neq -9; \) E(3;-9) не принадлежит гарфику \( 34^2=48 \neq -2 \) F(4;-2) не принадлежит гарфику \( 32^2=12 \neq -4 \) K(2;-4) не принадлежит гарфику На рисунке изображён график функции у=-х2+4.* Какие из данных прямых не имеют с графиком этой функции ни одной общей точки? Укажите их номера. 1) у=х; 2) у=х+5; 3) у=4; 4) х=-3; 5) у=10 y=x будет пересекаться, потому что y=x проходит через начало координат y=x+5 не будет, т.к. эта функция поднята вверх на 5 клеток y=4 тут будет одна точка, т.к. параллельно оси X и проходит через точку 4 x=-3 будет пересекаться т.к. внизу эта функция пересечёт параболу y=10 не будет, т.к. функция поднята вверх на 10 клеток и она параллельна к оси x Ответ: 2 и 5 Найдите все значения b, при которых график функции y=x^2-6х-b+3 имеет две общие точки с осью абцисс Чтобы эта парабола имела 2 общие точки с осью абсцисс, уравнение должно иметь 2 корня, т.е. дискриминант должен быть > 0 D=36-4(-b+3)>0, 36+4b-12>0, 4b>-24, b>-6. Ответ: (-6; +беск)