Найдите область значений функции \(y = x^2 - 8x - 11\), где x принадлежит (-2,5)

Y-2,5 -x-11-8*x-2,5-x

Y=x^2-8x-11
x принадлежит(-2;5)
функция Y=x^2-8x-11 на интервале от - беск до +4 монотонно убывает
от +4 до + беск - монотонно возрастает
+4 находится на интервале (-2;5)
значит если х принадлежит(-2;5), то min(Y) = Y(x=4)=4^2-8*4-11=-27
если х принадлежит(-2;5), то max(Y) = max(Y(x=-2);Y(x=5))
Y(x=-2)=(-2)^2-8*(-2)-11=9
Y(x=5)=(5)^2-8*(5)-11=-26
Ответ: если х принадлежит(-2;5), то Y принадлежит [-27;9)

Найдите область значений функции \(у=\sqrt{4-х^2} + \frac{3х}{х}\)

Так как на 0 делить нельзя, 1-х не может быть равно 0, значит х не может равняться 1. Подкоренное выражение не может быть отрицательным, значит, 12-4х-х^2>0
Решаем: -х^2-4х+12=0
D=16-4*(-1)*12=64
x1=(4-8)/-2=2
x2=(4+8)/-2=-6
x € [-6;1)¥(1;2]

Найдите область значений функции y=х^2-4х-7, где х принадлежит [-1;5]

График заданной функции y=х^2-4х-7  это парабола ветвями вверх.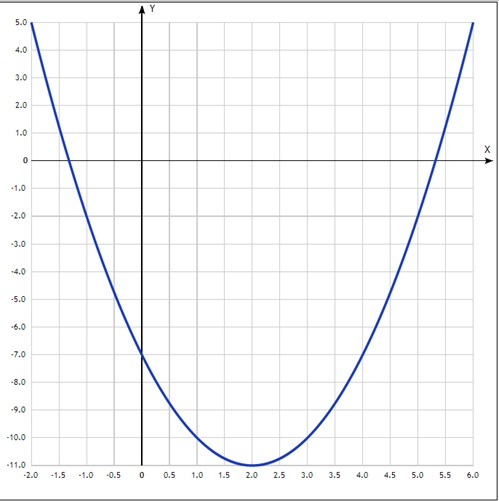
Вершина её Хо = -в/2а = 4/2 = 2, минимальное значение функции в вершине Уо = 2²-4*2-7 = 4-8-7 = -11.
При Х=-1 У = 1+4-7 = -2,
при Х =5 У = 25-20-7 = -2.

Отсюда ответ: х ∈ [-1;5], у ∈ [-11;-2].

Найти область определиния и множество значений функции y=2cosx

область определения:

функция  cosx   определена на всей числовой оси

2cosx также определяется по всей оси

                   D(y) = R

множество значений:           - 1   ≤    cosX    ≤     1                | *2

                                                    -2    ≤   2cosX  ≤     2

               =>   Е(у) = [-2;2]

Область определения: D(y)=R, то есть любое число

Область значений: D(y)=[-2; 2], так как cosx изменяется в [-1;1]

Укажите множество значений функции f(x)=4х^2+8х+5

Это парабола, ветви которой направлены вверх. Найдем координаты вершины: x0= - 8/8= - 1,

y0=4-8+5=1. Ниже точки (-1; 1) нет ни одной точки параболы, т.е. множество значений будет [1; +беск)