Исследовать на монотонность функцию \( f(x)=x^3(1-x) \)

Раскрывайте скобку, получите многочлен. Функция, представляющая собой многочлен, монотонна на всей области определения.

Находите производную и, приравнивая ее к нулю, находите критические точки:

\(3x^2 - 4x^3 = 0,\\х_1 = 0, x_2 = \frac{3}{4}\)

Определяете знаки производной на каждом из промежутков, на которые эти точки разбивают область определения данной функции.

На том промежутке, где производная положительна, исходная функция монотонно возрастает.

В нашем случае это промежуток от 0 до 3/4.

На том промежутке, где производная отрицательна, функция монотонно убывает.

В нашем случае это промежутки от минус бесконечности до нуля и от 3/4 до плюс бесконечности.

Исследуйте функцию f(x)=x2-4x-5 и постройте её график

Графиком функции является парабола, ветви которой направлены вверх.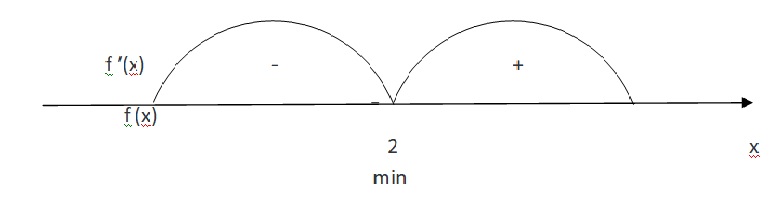
1) D (f) =R, т.к. f – многочлен.
2) f(-х) = (-х)2 - 4(-х)  - 5 = х2 + 4х – 5
 Функция поменяла знак частично, значит, f не является ни чётной, ни нечётной.
3) Нули функции: При х = 0 у = - 5; (0;-5) при у = 0 х2 - 4х – 5 = 0
По теореме, обратной теореме Виета х1 = -1; х2 = 5 (-1;0); (5;0).
4) Найдём производную функции f: f ′(х) = 2х – 4
Найдём критические точки: f ′(х) = 0;

2х – 4 = 0; х = 2 – критическая точка
5) Найдём промежутки монотонности: Если функция возрастает, то f'(х) > 0 ;  2х – 4 > 0; х > 2.
Значит, на промежутке (2; ∞) функция возрастает.
Если функция убывает, то f'(х) < 0; 2х – 4 < 0; х < 2.
Значит, на промежутке (- ∞; 2)  функция убывает.
6)  Найдём координаты вершины параболы: Х = Y =  22 - 4*2 – 5 = -9 (2;-9) – координаты вершины параболы.
7) Область изменения функции Е (у) = (-9; ∞)
 8) Построим график функции: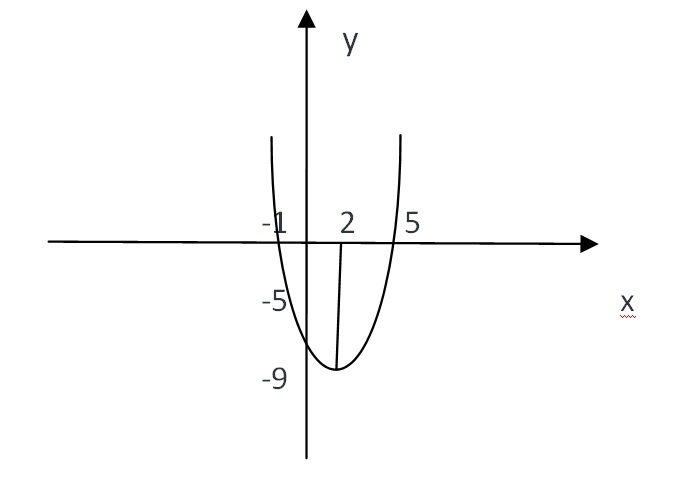
 

Исследование функции и построение ее графика: у=x^4-5x^2+6

Y=x^4-5x²+6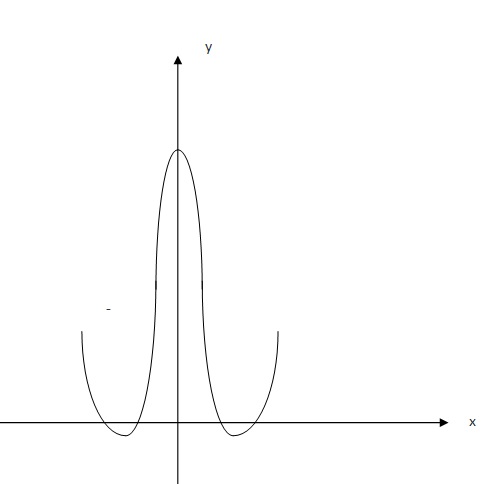
D(y)∈(-∞;∞)
y(-x)=x^4-5x²+6 четная
Точки пересечения с осями (-√3;0);(-√2;0);(√2;0);(√3;0);(0;6)
y`=4x³-10x=0
2x(2x²-5)=0
x=0 x=-√10/2 x=√10/2
  _ + _ +
-(-√10/2)-(0)-(√10/2)-
убыв min возр max убыв min возр
ymin=-1/4
ymax=6

Исследовать на экстремумы, точки перегиба и построить график функции y=((1/3)x^2)-4x

y = 1/3*x^2 - 4x

Найдём первую производную

y’ = 1/3*2x - 4

Найдём критические точки y'=0

1/3*2x - 4 = 0

2x = 12

x=6 -> точка минимума

Найдём вторую производную

y'' = (1/3*2x - 4)'  = 2/3  

Точек перегиба - нет, так как у 2/3=0 нет реш.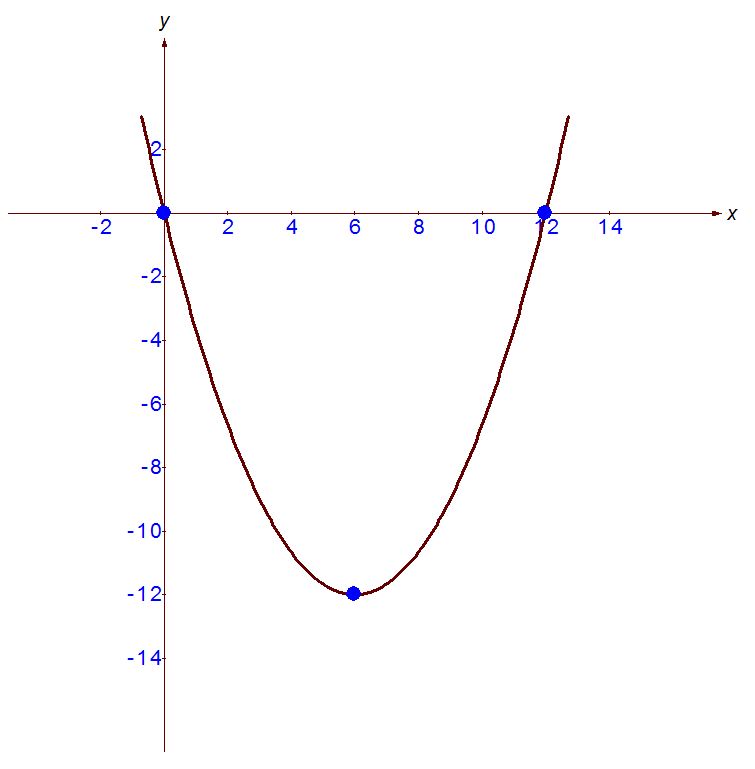

Сделайте полный анализ функции \( y=\frac{x^2}{x^2-1}\)

Область определения: (-INF;2)U(2;+INF)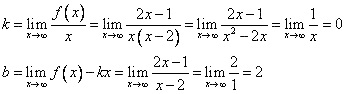
нули: (0;1/2);(1/2;0)
Асимптоты: вертикалная: x=2 Слева в минус бесконечность, справа в плюс.
Наклонная:  y=2
Производная: Функция везде убывает

Или есть еще вариант, посложнее...

Перечислить свойства функции y=|x|

Область определения - множество действительных чисел

Область значения от 0 включительно до плюс бесконечности

Парная функция

Непериодическая

Точки пересечения с осями координат (0:0)

от минус бесконечности до 0 убывающая

от 0 до плюс бесконечности возрастающая

положительная на множестве действительных чисел, за исключением точки 0

асимптоты отстуствуют

Свойства и график функции y = sin x

Свойства графика функции y=sin x.
1. Область определения функции множество действительных чисел: D(y)=R.
2. Множество значений - промежуток [-1;1]: E(у)=[-1;1].
3. Функция y=sin x является нечетной: sin(-a)=-sin a.
4. Функция периодическая, наименьший положительный период равен 2Π(пи): sin(a+2Π)=sin a.
5. График функции пересекает ось ОХ при а= Πn, n принадлежит Z.
6. Промежутки знакопостоянства: y > 0 при (2Πn+0;Π+2Πn),n принадлежит Z; у < 0 при (Π+2Πn;2Π+2Πn) n принадлежит Z.
7. Функция непрерывна и имеет производную при любом значении аргумента: (sin x)'=cos x.
8. Функция у=sin а возрастает при а принадлежит (-Π/2+2Πn; Π/2+2Πn), n принадлежит Z. И убывает при а принадлежит (Π/2+2Πn;3Π/2+2Πn), n принадлежит Z.
9. Функция имеет минимум при а= -Π/2+2Πn, n принадлежит Z. И максимум при а = Π/2+2Πn, n принадлежит Z.