| Главная Научный калькулятор | |
|
|
Теорема синусов. Формула Герона.Рассмотрим треугольник АВС с высотой СН = h, опущенной из вершины С. Площадь треугольника равна половине произведения высоты на основание S=1/2ch. Высоту можно выразить из прямоугольного треугольника АНС как h = bsina в случае острого угла a или как h = bsin(p-a) в случае тупого угла a.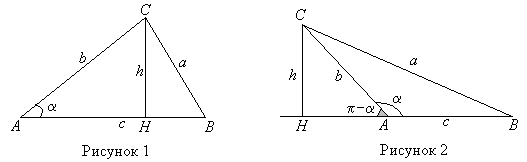 В силу равенства sin(p-a) = sina в обоих случаях имеем h = bsina. Формула для площади треугольника примет вид S=1/2 * b * c * sinα(1)
Теорема 33. Площадь треугольника равна половине произведения двух его
сторон и синуса угла между ними.Записав эту формулу и для других сторон, мы увидим, что вы из них вытекают следующие пропорции выражающие следующую теорему. Теорема 34. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Причем, последнее равенство взято (доказ.) в теме описанная около треугольника окружность из теорем 40 и d6 Выведем теперь формулу Герона, дающую выражение площади треугольника через длины его сторон. Для этого из формулы теоремы косинусов выразим cosα, а из теоремы синусов sinα: 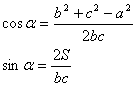
(3) (4) Вспомним главное тригонометрическое тождество. Возводя оба последних равенства в квадрат и складывая их почленно, получаем 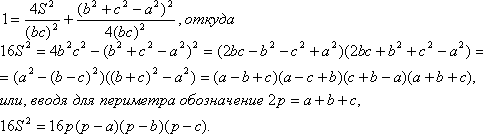 И окончательно получаем Теорема 35. Формула Герона. Площадь треугольника можно вычислить по следующей формуле: Отсюда получаются также формулы для высот треугольника: Достаточно, конечно, знать на память формулу Герона, так как выражения для высот получаются из неё немедленно. |