| Главная Научный калькулятор | |
|
|
Задача №147В правильной четырехугольной пирамиде сторона основания равна 12 см, угол наклона боковых граней 60. Через сторону основания под углом 45 к основанию проведено сечение, найти площадь сечения.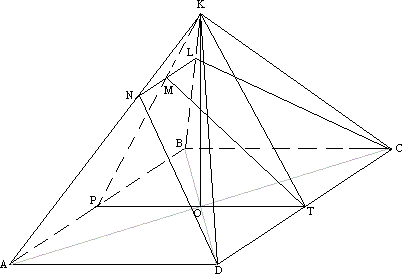 Сделаем дополнительные построения. Проведем высоту и через основание высоты О проведем прямую параллельно стороне основания. Через прямые КО и РТ проведем плоскость (она определена и единственна по третей аксиоме). Т.к плоскость РКТ проходит через прямую КО, перпендикулярную плоскости основания АВСD, то эти плоскости перпендикулярны по признаку перпендикулярности плоскостей. Воспользуемся еще одной теоремой из той же темы: Если в одной из перпендикулярных плоскостей провести прямую, перпендикулярную линии их пересечения, то эта прямая перпендикулярна второй плоскости. DT перпендикулярна РТ по построению, значит DT перпендикулярна и КТ. Угол КТР является линейным углов двугранного угла между основанием АСВD и боковой гранью KDC. Теперь в плоскости КРТ через точку Т проведем прямую ТМ, образующую с РТ угол 45о. Затем в плоскости АВК через точку М проведем параллельно АВ прямую LN. Прямая LN параллельна DC по признаку параллельности прямых: две прямые параллельные третей прямой параллельны между собой. Через параллельные прямые NL и DC проведем плоскость (она определена и единственна). Мы постоили плоскость NLCD, составляющую с плоскостью основания 45 градусов. Рассмотрим плоскость КРТ: 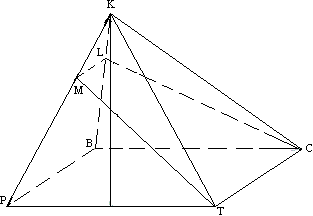 Сторона РТ треугольника КРТ равна стороне основания т.е. 12 см., а сам треугольник КРТ равносторонний, т.к. два его угла равны 60 градусов (по данным). Поэтому все его стороны по 12 см.
Для треугольника РМТ запишем теорему синусов:
Сторона РТ треугольника КРТ равна стороне основания т.е. 12 см., а сам треугольник КРТ равносторонний, т.к. два его угла равны 60 градусов (по данным). Поэтому все его стороны по 12 см.
Для треугольника РМТ запишем теорему синусов: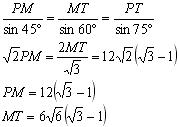 Рассмотрим грань АВК. Здесь КР ось симметрии. Треугольники КРВ и KML прямоугольные и подобны по острому углу РКВ. Поэтому: 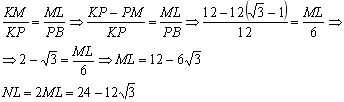 Наше сечение суть - трапеция. DC перпендикулярна плоскости КРТ, т.к. перпендикулярна двум её прямым РТ и КТ (ранее доказано) по признаку перпендикулярности прямой и плоскости. Значит DC перпендикулярна и МТ. Т.е. МТ - высота трапеции NLCD. Найдем её площадь по формуле: 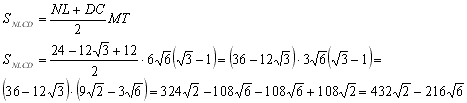
|