| Главная Научный калькулятор | |
|
|
Задача №157Основанием прямого параллелипипеда служит ромб АBCD. Сторона ромба равна а, один из его углов - альфа. Боковое ребро параллелипипеда равно а. Вычислите длины диагоналей параллелипипеда и расстояние между его ребрами ВС и АD.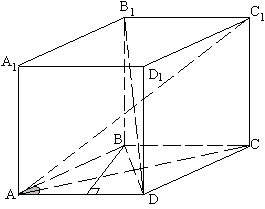 Для нахождения диагоналей параллелипипеда найдем диагонали основания.
Для нахождения диагоналей параллелипипеда найдем диагонали основания. 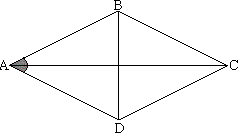 Треугольник ABD - равнобедренный (АВ=АD - стороны ромба), поэтому ∠ABD=∠ADB=(180°-α)/2=90°-α/2 Применим теорему синусов: 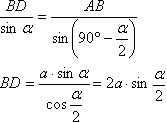 Рассмотрим треугольник АВС. По четвертому свойству (св-во диагоналей) ромба ∠ВАС=∠ВСА=α/2 Применим теорему синусов: 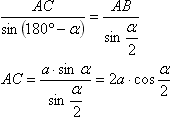 Теперь соответственно из треугольников АС1С и DВ1В по теореме Пифагора: 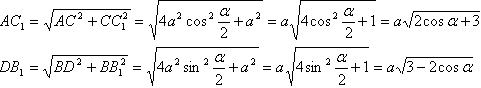 Для нахождения расстояния между ребрами ВС и АD (высота основания) расмотрим треугольник АВD и его высоту. Получим: h=asinα |