| Главная Научный калькулятор | |
|
|
Задача №211Дан треугольник АВС. АВ = 8, ВС = 4, АС = 6. Найти площадь треугольника АВС, а также радиус вписанной, радиус описанной окружностей, высоту, проведённую из угла В, медиану и биссектрису, проведённые также из угла В.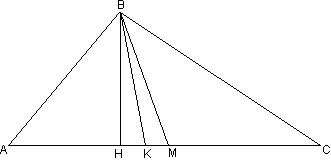 Для нахождения площади применим формулу площади через половину произведения высоты и стороны:
Для нахождения площади применим формулу площади через половину произведения высоты и стороны:
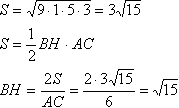 Найдем медиану. Обозначим длины сторон, лежащих против вершин А,В и С, соответственно a, b, c. Пусть BM - медиана треугольника АВС. Обозначим BМ=m, ∠BМА=α, тогда ∠СМВ=180о - α Из треугольников АBМ и СМВ по теореме косинусов будем иметь: 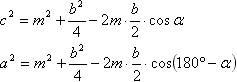 Складывая почленно два этих равенства и учитывая, что cos(180° - α)=-cosα, получаем: 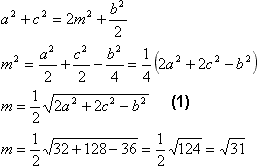 Найдем биссектрису ВК. Обозначим BК=l, ∠АВК=β. Учитывая, что биссектриса делит угол пополам: ∠СВК=∠АВК=β, а ∠АВС = ∠СВК+∠АВК=2β. Воспользуемся таким свойством: биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам (доказательство): 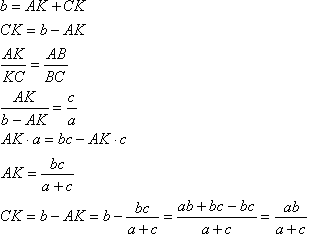 Применим в треугольниках АВК и СВК теорему косинусов: 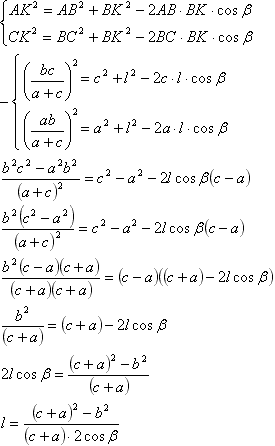 Используя теорему косинусов в треугольнике АВС, найдем cosβ: 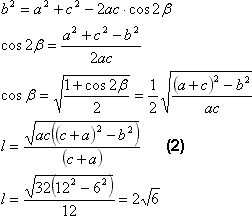
|