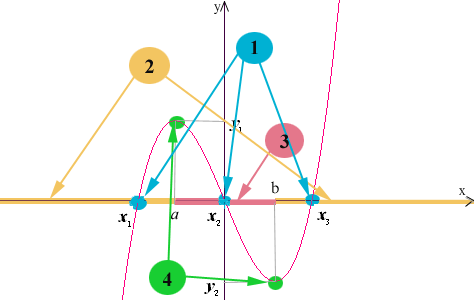
Промежутки 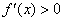и называются промежутками возрастания функции. Для каждой внутренней точки промежутка возрастания должно выполняться условие . На рисунке на этих промежутках график идет снизу вверх.

Значения X1, X2, X3 называются нулями функции и определяются из условия ƒ(x)=0. На рисунке - это абсциссы точек пересечения графика с осью х.

Промежуток AB называется промежутком убывания функции. Для каждой внутренней точки промежутка убывания должно выполняться условие 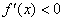. На рисунке на этих промежутках график идет сверху вниз.

Значение Y1 называется точкой максимума функции, а Y2 - точкой минимума, соответствующие значения функции a и b называются максимумом и минимумом функции. Максимумы и минимумы функции называются ее экстремумами. Для нахождения точек экстремума функции поступают следующим образом. Вначале выявляют точки, "подозрительные" на экстремум (критические точки функции). Это те точки, в которых прозводная функции равна нулю или не существует. Для того, чтобы критическая точка была точкой масимума нужно, чтобы производная при переходе через эту точку меняла знак с "+" на "-", а для точки минимума с "-" на "+". На рисунке в этих точка график имеет "холмик" или "впадину". Если же при переходе через критическую точку производная не меняет знака, то в малой окрестности этой точки график функции идет почти горизонтально (касательная к графику параллельна оси абсцисс). На данном рисунке таких точек нет.