| Главная Научный калькулятор | |
|
|
Исследование функции с помощью второй производной.
На рисунке изображен график функции. Свойства функции, которые необходимо выявить в ходе исследования, отмечены номерами в кружках. Для того, чтобы вспомнить, как определить те или иные свойства функции, отраженные на графике, щелкните мышкой по нужному номеру. 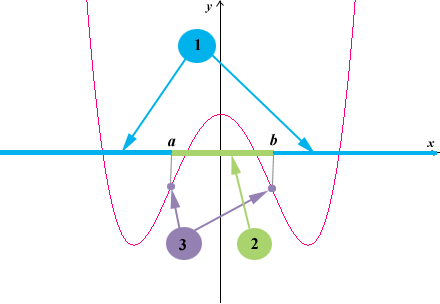
На промежутках
На промежутке [a, b] график функции направлен выпуклостью вверх. Касательные к графику функции, проведенные во внутренних точках этих промежутков, в некоторой окрестности точки касания располагаются выше графика. В каждой внутренней точке таких промежутков
Точки графика функции
|