| Главная Научный калькулятор | |
|
|
УглыСодержание:
Определение.1. УголОпределение 1.1. Угол (альтернативное определение) Определение.2. Развернутый угол Определение.3. Прямой угол Определение.4. Острый угол Определение.5. Тупой угол Определение.6. Смежные углы Определение.7. Вертикальные углы Теорема.1. Сумма смежных углов Теорема.2. Вертикальные углы Определение.8. Биссектриса угла Теорема.3. Свойство биссектрисы угла Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом. Определение 1.1. Углом называют фигуру, состоящую из точки - вершины угла - и двух различных полупрямых, исходящих из этой точки, - сторон угла. Например, угол ВОС на рис1 Рассмотрим сначала две пересекающиеся прямые. При пересечении прямые образуют углы. Есть частные случаи: Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым. Определение 3. Прямой угол - это угол величиной в 90 градусов. Определение 4. Угол, меньший 90 градусов, называется острым углом. Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом. Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными. Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами. На рисунке 1: смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1 вертикальные: 1 и 3; 2 и 4 Теорема 1. Сумма смежных углов равна 180 градусов. Для доказательства рассмотрим на рис 1 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов. Теорема 2. Вертикальные углы равны. Для доказательства рассмотрим на рис 1 вертикальные углы АОВ и DОС. Запишем для смежных углов теорему 1: ∠АОВ+∠ВОС=180о ∠DОС+∠ВОС=180о, откуда ∠АОВ=180о-∠ВОС ∠DОС=180о-∠ВОС, откуда ∠АОВ=∠DОС, ч.т.д. Определение 8. Биссектрисой угла называют луч, который исходит из вершины угла, проходит между его сторонами и делит его пополам. 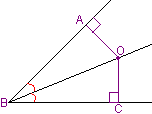 Теорема 3. Все точки биссектрисы угла равноудалены от его сторон.
Теорема 3. Все точки биссектрисы угла равноудалены от его сторон.Докажем это утверждение на примере точки О. Проведем перпендикуляры ОА и ОС - обозначим расстояния от точки до сторон угла. Прямоугольные треугольники АВО и СВО равны по острому углу и гипотенузе (∠АВО=∠СВО по определению, а ОВ - общая). Поэтому равны и соответственные катеты: ОА=ОС, ч.т.д. |