Шар и сфера

Определение 1. Сфера радиуса R есть множество точек пространства, удаленных от данной точки на положительное расстояние R.
В координатном пространстве сфера с центром O(a;b;c) и радиусом R задается уравнением: Сфера является фигурой вращения. При вращении полуокружности радиуса R вокруг её диаметра получаеся сфера радиуса R.
Теорема 1. Сечение сферы радиуса R плоскостью, отстоящей от её центра на расстояние d, 0£d<R, есть окружность радиуса r, причем: Теорема 2. Сечения, равноудаленные от центра сферы, имеют равные радиусы.
Определение 2. Сечение сферы плоскостью, проходящей через её центр (d=0) называется большой окружностью.
Если центр сферы не лежит в плоскости сечения (0<d<R), то
Теорема 3. Прямая, проходящая через центр сферы и центр окружности сечения, перпендикулярна плоскости сечения
Теорема 4. Через любые четыре точки, не лежащие в одной плоскости, можно провести сферу и притом только одну.
Определение 3. Многогранник называется вписанным в сферу (а сфера описанной около многогранника), если все вершины многогранника лежат на сфере.
Определение 4. Сфера называется вписанной в многогранный угол (а многогранный угол описанным около сферы), если она касается каждой его грани. Определение 4. Сфера называется вписанной в многогранник (а многогранник описанным около сферы), если она касается всех его граней.
Определение 5. Шар радиуса R есть геометрическое место точек пространства, удаленных от данной точки не более чем на расстояние R (R>0).

Определение. Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние - радиусом шара. Шаровой или сферической поверхностью называется геометрическое место точек пространства, равноудаленных от центра шара на заданное расстояние — радиус шара.

Теорема. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центрана секущую плоскость.
Доказательство. Пусть α - секущая плоскость и О — центр шара. Опустим перпендикуляр из центра шара на плоскость о и обозначим через О' основание этого перпендикуляра. Теперь возьмем точки A и B, принадлежащие сфере шара, и плоскости α. Соединим O' и A. Соединим O' и B. OO' перпендикулярна 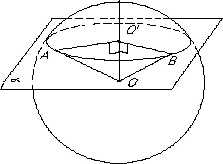плоскости O. (по построению), значит она перпендикулярна и любой прямой в этой плоскости, то есть перпендикулярна OA и O'B, =>треугольники OOOA и OO'B перпендикулярные. Они равны по катету и гипотенузе (OO' — общая, OA=OB — радиусы шара). Из равенства треугольников следует равенство соответствующих сторон, то есть O'A = O'B. Таким образом можно доказать, что точка O' равноудалена от всех точек фигуры, образовавшейся при пересечении плоскости и шара. А так как точка O' и все равноудаленные от нее точки находятся в одной плоскости, то можно заключить, что эта фигура — окружность. А если взять еще и все точки плоскости ех заключенные в этой окружности, то получится круг.

Определение. Плоскость, имеющая с шаром одну единственную общую точку, называется касательной к этому шару.

Теорема Радиус, проведенный в точку касания шара с плоскостью, перпендикулярен этой плоскости.
Доказательство. Пусть α - касательная плоскость и А — точка касания, О — центр шара. Возьмем в плоскости α точки B и C, не совпадающие с точкой A и между собой. Отрезки OC и OB пересекают шар 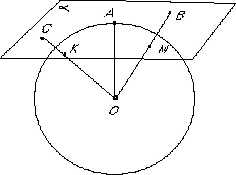соответственно в точках K и M. OC = OK+KC = R + KC>OA=ROB = OM + MB = R+MB>OA=R Видно, что OA — самое короткое расстояние от точки O до плоскости α. По определению, самым коротким расстоянием от точки до плоскости является перпендикуляр, опущенный из этой точки на плоскость. Значит, отрезок OA перпендикулярен плоскости α. Ч.т.д.

Теорема Плоскость, перпендикулярная радиусу и проходящая через его конец, лежащий на сфере, является касательной к этой сфере. Доказательство сводится к тому, что надо показать, что эта плоскость и сфера имеют только одну общую точку. 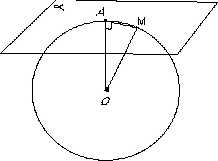Пусть дана сфера с центром в точке O и радиусом OA. Плоскость α перпендикулярна радиусу OA. Пусть сфера и плоскость α имеют еще одну общую точку M OA=OM=R. Соединим точки M, A и O. По условию OA перпендикулярен плоскости α, а значит, перпендикулярен и любой прямой этой плоскости, то есть OA перпендикулярен AM. В треугольнике AOM угол OAM прямой, значит треугольник прямоугольный, и в нем OA — катет, OM — гипотенуза. Как известно, гипотенуза всегда больше катета, то есть OM>OA а значит, OM больше OA, как предполагалось. Следовательно, точка М не лежит на сфере. Таким образом, доказано, что ни одна точка плоскости α, кроме точки A, не лежит на сфере.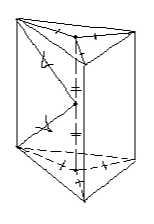

Сфера называется описанной около многогранника, если все вершины многогранника лежат на сфере. Центром этой сферы является точка, равноудаленная от всех вершин многогранника. Около призмы можно описать сферу тогда и только тогда, когда призма прямая и около её основания можно описать окружность. Центром сферы, описанной около призмы, является середина отрезка, соединяющего центры описанных около оснований окружностей. Если призма четырехугольная, то её основание должно обладать тем свойством, что сумма противоположных углов равна 130°. Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность. Центр сферы, описанной около пирамиды, перпендикулярен к плоскости основания пирамиды, восстановленном из центра окружности, описанной около основания пирамиды. Если боковые ребра пирамиды равнонаклонены к основанию, то вершина пирамиды проектируется в центр описанной около основания окружности. В этом случае около пирамиды всегда можно описать сферу. Центром этой сферы является точка пересечения высоты пирамиды и плоскости, перпендикулярной боковому ребру и проходящей через его середину.

Объем и площади частей сферической поверхности