| Главная Научный калькулятор | |
|
|
ЦилиндрРассмотрим какую-либо линию (кривую, ломаную или смешанную) l, лежащую в некоторой плокости a, и некоторую прямую S, пересекающую эту плоскость. Через все точки данной линии l проведем прямые, параллельние прямой S; образованная этими прямыми поверхность b называется цилиндрической поверхностью. Линия l называется направляющей этой поверхности, прямые s1, s2, s3,... - её образующими.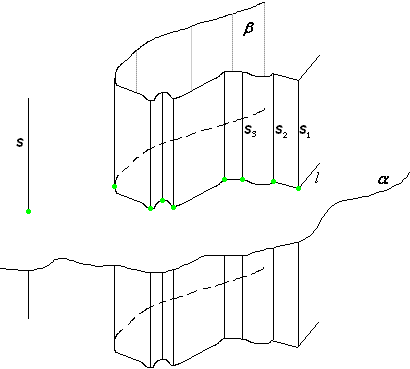 Если рассечь любую цилиндрическую поверхность произвольной плоскостью, не параллельной её образующим, то получим линию, которая также может быть принята за направляющую данной поверхности. Среди направляющих выделяется та, которая получается от сечения поверхности плоскостью, перпендикулярной образующим поверхности. Такое сечение называется нормальным сечением, а соответствующая направляющая - нормальной направляющей. Если направляющая - замкнутая (выпуклая) линия (ломаная или кривая), то соответствующая поверхность называется замкнутой (выпуклой) призматической или цилиндрической поверхностью. Из цилиндрических поверхностей простейшая имеет своей нормальной направляющей окружность. Рассечем замкнутую выпуклую призматическую поверхность двумя плоскостями, параллельными между собой, но не параллельными образующим. 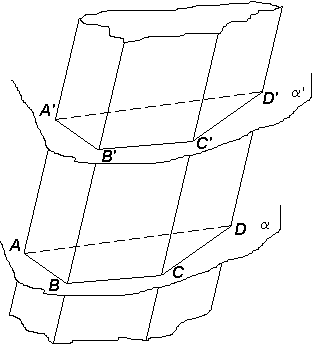 В сечениях получим выпуклые многоугольники. Теперь часть призматической поверхности, заключенная между плоскостями a и a', и две образовавшиеся при этом многоугольные пластинки в этих плоскостях ограничивают тело, называемое призматическим телом, короче, призмой.
В сечениях получим выпуклые многоугольники. Теперь часть призматической поверхности, заключенная между плоскостями a и a', и две образовавшиеся при этом многоугольные пластинки в этих плоскостях ограничивают тело, называемое призматическим телом, короче, призмой. Цилиндрическое тело, короче, цилиндр определяется аналогично призме: Цилиндром называется тело, ограниченное с боков замкнутой (выпуклой) цилиндрической поверхностью, а сторцов двумя плоскими параллельными основаниями. Оба основания цилиндра равны, также равны между собой и все образующие цилиндра, т.е. отрезки образующих цилиндрической поверхности между плоскостями оснований. Цилиндр называется прямым, если плоскости его оснований перпендикулярны к образующим. Мы изучим только прямой круговой цилиндр, называемый также цилиндром вращения. Прямым круговым называется прямой цилиндр, осонованиями которого являются круги Он может быть образован вращением прямоугольника вокруг одной из своих сторон. Радиус основания называется радиусом цилиндра, образующая одновременно служит высотой. |