| Главная Научный калькулятор | |
|
|
Перпендикуляр и наклоннаяСодержание:
Определение.1. ПерпендикулярОпределение.2. Наклонная Теорема.1. Перпендикуляр из точки вне прямой Теорема.2. Перпендикуляр из точки принадлежащей прямой Теорема.3. Основное свойство серединного перпендикуляра к отрезку Теорема.4. Следствие теоремы 3 Определение 1. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку пересечения. Конец отрезка, лежащий на данной прямой, называется основанием перпендикуляра. 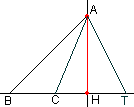 Определение 2. Наклонной, проведенной из данной точки к данной прямой, называется отрезок, соединяющий данную точку с любой точкой прямой, неявляющейся основанием перпендикуляра, опущенного из этой же точки на данную прямую.
Определение 2. Наклонной, проведенной из данной точки к данной прямой, называется отрезок, соединяющий данную точку с любой точкой прямой, неявляющейся основанием перпендикуляра, опущенного из этой же точки на данную прямую.На рисунке АН - перпендикуляр, АВ, АС, АТ - наклонные. Расстоянием между точками является длина отрезка, соединяющего эти точки. Точка называется равноудаленной от двух и более данных точек, если растояния от этой точки до каждой данной точки равны. Расстоянием от точки до прямой является длина перпендикуляра опущенного из донной точки на данную прямую. Точка называется равноудаленной от двух и более прямых, если растояния от этой точки до каждой прямой равны. Теорема 1. Из точки, не принадлежащей данной прямой, можно провести перпендикуляр к этой прямой, причем только один. Теорема 2. Из данной точки прямой можно восстановить перпендикуляр, причем только один. Теорема 3. Любая точка перпендикуляра, проходящего через середину данного отрезка, равноудалена от его концов. Доказательство: Пусть AB - отрезок, C - его середина, и H - произвольная точка на серединном перпендикуляре. Тогда углы HCA и HCB прямые, HC = HC, AC = BC. Значит, треугольники ACH и BCH равны. Следовательно, их стороны AH и BH равны. Что и требовалось доказать. Теорема 4. Если данная точка равноудалена от концов отрезка, то она лежит на прямой, перпендикулярной данному отрезку и проходящей через его середину. |