Теорема 1. Теорема о трех перпендикулярах. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной.
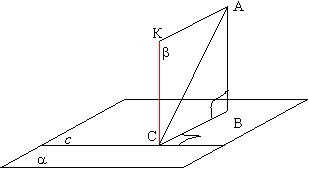Доказательство.
Пусть АВ – перпендикуляр к плоскости a, АС – наклонная и с -прямая в плоскости a, проходящая через основание наклонной СK. Проведем прямую СК, параллельно прямой АВ. Прямая СК перпендикулярна плоскости a (по тореме 2, так как она параллельна АВ), а значит и любой прямой этой плоскости, следовательно, СК перпендикулярна прямой с.
Проведем через параллельные прямые АВ и СК плоскость b (параллельные прямые определяют плоскость, причем только одну). Прямая с перпендикулярна двум прямым лежащим в плоскости b, это ВС по условию и СК по построению, значит она перпендикулярна и любой прямой, принадлежащей этой плоскости, а, значит, перпендикулярна и прямой АС. Другими словами наклонная АС перпендикулярна прямой с, лежащей в плоскости a.

Теорема 2. Обратная теореме о трех перпендикулярах. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции.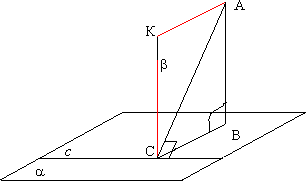

Доказательство. Пусть АВ – перпендикуляр к плоскости a, АС – наклонная и с – прямая в плоскости a, проходящая через основание наклонной С. Проведем прямую СК, параллельно прямой АВ. Прямая СК перпендикулярна плоскости a (по тореме 2, так как она параллельна АВ), а значит и любой прямой этой плоскости, следовательно, СК перпендикулярна прямой с. Проведем через параллельные прямые АВ и СК плоскость b (параллельные прямые определяют плоскость, причем только одну). Прямая с перпендикулярна двум прямым лежащим в плоскости b, это АС по условию и СК по построению, значит она перпендикулярна и любой прямой, принадлежащей этой плоскости, значит перпендикулярна и прямой ВС. Другими словами, проекция ВС перпендикулярна прямой с, лежащей в плоскости a.