| Главная Научный калькулятор | |
|
|
Дифференциальные уравненияУравнения, которые содержат аргумент, функцию этого аргумента и производные этой функции до некоторого порядка включительно, называют дифференциальными, а наивысший порядок производной, входящей в такое уравнение, - порядком этого уравнения.Решения дифференциальных уравнений.Решением дифференциального уравнения называют любую функцию, при подстановке которой в это уравнение получается тождество. График решения дифференциального уравнения называют интегральной кривой этого уравнения.Простейшими являются дифференциальные уравнения вида y'=f(x). Чтобы решить их, надо найти функцию у по её производной f(x):
у=of(x)dx
Если F - одна из первообразных для f, то это равенство записывается так:
y=F(x)+C
Функцию y=j(x,C), где С - произвольная постоянная, называют общим решением дифференциального уравнения y'=f(x,y) в области W, если- для любого С она является решением этого уравнения, т.е. j'(x,C)=f(x,j(x,C)); - для любой точки М0(х0,у0) из области W существует единственное решение С0, при котором линия у=j(x,C0) проходит через точку М0, т.е. у0=j(x0,C0). Решение дифференциального уравнения, получаемое из общего решения путем придания определенного значения произвольной постоянной, называют частным решением этого уравнения. Наряду с частными решениями дифференциальное уравнение может иметь решения, не получаемые из общего ни при каком значении произвольной постоянной. Такие решения называют особыми. Например, общее решение дифференциального уравнения (y')2+y2=1 имеет вид: y=sin(x+C) - семейство синусойд. Кроме того, это уравнение имеет два особых решния: у=-1 и у=1. Рассмотрим теперь дифференциальные уравнения второго порядка. Простойшими из них являются уравнения вида: y''=f(x).
Чтобы решить такое уравнение, введем новую функцию z=y'. Тогда имеем z'=(y')'=y'', и уравнение примет вид: z'=f(x). Из него находим:
z=of(x)dx=F(x)+C1,
где F - одна из первообразных функции f, C1 - произвольная постоянная. Но z=y', и потому имеем: y'=F(x)+C1. Значит,y=o(F(x)+C1)dx=F(x)+C1x+C2,
где F - одна из первообразных функции F, а С2 - вторая поизвольная постоянная.
В решение уравнения первого порядка входит одна произвольная постоянная, а в решение уравненя второго порядка - две произвольные постоянные. Это верно и для уравнений более общего вида: общее решение дифференциального уравнения n-го порядка зависит от n произвольных постоянных.Уравнения с разделяющимися переменными.К операции интегрирования сводится и решение дифференциального уравнения первого порядка вида (1):y'=j(x)y(у)
в левой части - производная искомой функции, в правой - произведение двух функций, из которых одна зависит от х, а другая - от у.Если при у=у0 функция y обращается в нуль, т.е. y(y0)=0, то функция у=у0 является одним из решений данного уравнения. В самом деле, подставляя в уравнение у0 вместо у, получаем равенство (у0)'=j(x)y(y0). Оно тождественно выполняется при любом значении х, т.е. (у0)'=0 (производная постоянной равна 0), а y(у0)=0 по условию. В области, где y(у) не равно нулю, данное уравнение (1) равносильно уравнению y'/y(y) = j(x). Умножим обе части этого уравнения на dx и учтем, что y'dx=dy. Получаем уравнение (2) 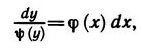 Перейдем к решению уравнения (2). Если F - первообразная функции j, а Y - первообразная функции 1/y, то dF(x)=F'(x)dx=j(x)dx, dY(y)=Y'(y)dy=(1/y(y))dy=dy/y(y). Значит, уравнение (2) можно записать так: dY(y)=dF(x).
Здесь слева и справа стоят дифференициалы функций, зависящих от х (ведь у является некоторой функцией от х). Эти дифференциалы равны друг другу лишь в случае, когда сами функции отличаются лишь на постоянное слагаемое, т.е. когда Y(у)=F(x)+С. Но это равенство можно записать так:
 |