| Главная Научный калькулятор | |
|
|
Задача №143Основанием пирамиды KABCD является квадрат КАВС, сторона которого равна 12 см. Ребро CD перпендикулярно плоскости основания. Большее боковое ребро пирамиды наклонено к плоскости основания под углом 45 градусов. Через вершины А и С основания пирамиды проведено сечение параллельно ребру KD. Вычислите объем пирамиды, площадь сечения и объем пирамиды, отсекаемой от данной пирамиды плоскостью сечения.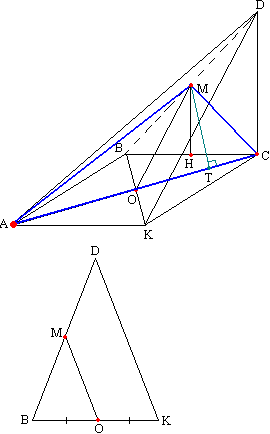 Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой этой плоскости, поэтому DC перпендикулярна ВС, АС и КС, т.е. треугольники BCD, ACD и KCD прямоугльные. Катет АС треугольника АСD больше катетов ВС и КС двух других, а CD общий катет. Поэтому гипотенуза AD треугольника АСD больше гипотенуз BD и KD треугольников ВСD и КСD соответственно, т.е. является самым большим боковым ребром пирамиды, и вот оно наклонено к плоскости основания под углом 45 градусов.
Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой этой плоскости, поэтому DC перпендикулярна ВС, АС и КС, т.е. треугольники BCD, ACD и KCD прямоугльные. Катет АС треугольника АСD больше катетов ВС и КС двух других, а CD общий катет. Поэтому гипотенуза AD треугольника АСD больше гипотенуз BD и KD треугольников ВСD и КСD соответственно, т.е. является самым большим боковым ребром пирамиды, и вот оно наклонено к плоскости основания под углом 45 градусов.Сделаем некоторые вычисления: 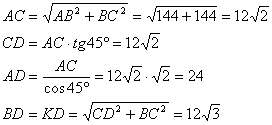 Последнее равенство следует из равенства прямоугольных треугольников ВСD и KCD по двум катетам (CD-общая, ВС=КС-стороны квадрата). Теперь вычислим обьём пирамиды по высоте CD и площади основания АВСК: 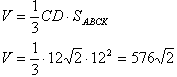 Учитывая, что диагонали квадрата равны и точкой пересечения делятся пополам ВК=АС и ВО=ОК. Расмотрим треугольник ВКD. В нем через точку О проведем прямую ОМ параллельно КD. По теореме о том, что параллельные линии отсекают на сторонах угла пропорциональные отрезки получаем, что ВМ=МD. МО - средняя линия треугольника КВD, т.к. проходит через середины сторон ВК и ВD. Средняя линия треугольника равна половине стороны, которую она не пересекает. Через точку М и прямую АС проведем плоскость, используя теорему: через прямую и нележащую на ней точку можно провести плоскость причем только одну. Также вспомним теорему: если прямая (не лежащая в данной плоскости) параллельна хотя бы одной прямой в этой плоскости, то она параллельна и всеё этой плоскости. Прямая КD параллельна МО по постоению, а значит параллельна плоскости МАС. Таким образом, мы построили нужное сечение. Рассмотрим прямоугольный треугольник ВDС: здесь СМ - медиана. Теорема - медиана гипотенузы прямоугольного треугольника равна её половине. 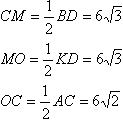 Таким образом, треугольник МОС равнобедренный (СМ=МО). По свойству равнобедренного треугольника, высота проведенная к основанию является также и медианой, т.е. ОТ=ТС 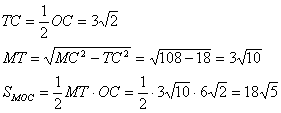 Нужно заметить, что МО является медианой треугольника АМС. Теорема - медиана треугольника делит его на два равновеликих треугольника: Плоскость ВDC проходит через прямую DC перпендикулярную плоскости АВСК, поэтому эти плоскости перпендикулярны. Из точки М опустим перпендикуляр МН на ВС. По теореме о том, что параллельные линии (МН параллельно DC, т.к. перпендикулярны одной прямой ВС) отсекают на сторонах угла пропорциональные отрезки получаем, что ВН=НС. Т.е. МН являтеся средней линией треугольника ВСD и равна половине DC. Также МН перпендикулярна плоскости АВС по теореме: если в одной из двух перпендикулярных плоскостей проведена прямая, перпендикулярная линии их пересечения, то эта прямая перпендикулярна второй плоскости. Т.е. МН является высотой пирамиды МАВС. Найдем обьем: 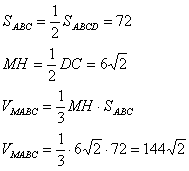 По задаче советую просмотреть темы: прямоугольный треугольник. |