Задача №166

Две окружности радиусов R и 3R внешне касаются друг друга в точке М. Их общая внешняя касательная касается их в точках А и В. Найти площадь криволинейного треугольника МАВ между внешней касательной и дугами окружности.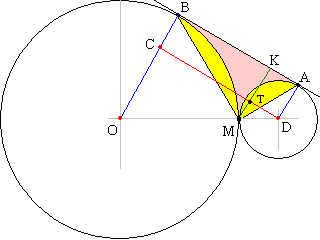
Для начала докажем, что центры и точка касания двух окружностей (как внешне, так и внутренне, но внутренне не будем трогать) лежат на одной прямой.
Через точку касания окружностей проведем касательную к одной из окружностей. Эта прямая будет также касательной и для второй окружности (по определению). Проведем радиусы в точку касания. Как известно радиус проведенный в точку касания перпендикулярен касательной. Мы имеем два перпендикуляра, проведенных к одной точке. Как известно, из одной точки на прямой можно поднять только один перпендикуляр. Поэтому радиусы продолжают друг друга или лежат на одной прямой. Т.е. точка М принадлежит OD.
Из точки М опустим перпендикуляр МК на АВ. Из точки D опустим перпендикуляр DC на ОВ. Он пересечет МК в точке Т.
Четырехугольник АВСD - прямоугольник (в нем все углы прямые по построению). Поэтому АВ=CD и AD=BC=R. Также ТК=ВС=R (ТКВС - прямоугольник также). ОС=ОВ-ВС=2R. MT=MK-TK=MK-R. OD=OM+DM=4R.
Прямоугольные треугольники ОСD и MTD подобны (общий острый угол), поэтому:
ОС:МТ=OD:MD
2R:(MK-R)=4R:R
2R=4MK-4R
6R=4MK
MK=3/2R
Из прямоугольного треугольника ОCD: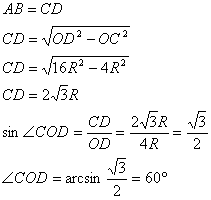

Углы СОD и АDО являются внутренними односторонними для параллельных прямых ОВ и DA. Поэтому ∠АDО=180°-∠СОD=120°
Найдем площади сегментов АМ и ВМ, обозначенных на рисунке желтым: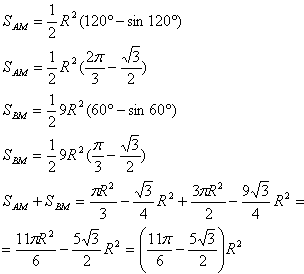

Найдем площадь треугольника АВМ, а затем и площадь искомой фигуры: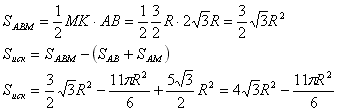