Задача №169

Дана четырехугольная пирамида SABCD Точка О - точка пересечения медиан треугольника SBD. Построить точку пересечения прямой, проходящей через точки C и O, с плоскостью, содержащей треугольник SAB.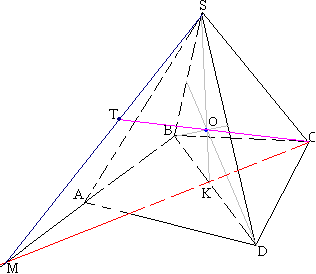
Обозначим основание медианы, проведенной из вершины S в треугольнике SBD за К. Продолжим АВ в сторону точки А. Проведем прямую через точки С и К и продолжим её до пересечения с прямой АВ. Точку их пересечения обозначим за М. Соединим точки S и М.
Точка О принадлежит прямой SК по данным, а значит принадлежит и плоскости SCK. Точка М принадлежит прямой СК (по построению), а значит принадлежит и плоскости SСК. Прямая SМ принадлежит плоскости SСК. Продолжим СО в сторону точки О до пересечения с SM. Обозначитм точку пересечения за Т.
Также точка М принадлежит прямой АВ (по построению), а значит принадлежит и плоскости SАВ. Прямая SМ принадлежит плоскости SАВ. Значит, точка Т тоже принадлеит плоскости SАВ. Другими словами, прямая СО перечекает плоскость SАВ в точке Т.