| Главная Научный калькулятор | |
|
|
Задача №193Из точек А и В лежащих в двух перпендикулярных плоскостях опущены перпендикуляры АС и BD на прямую пересечения плоскостей. Найдите длину отрезка АВ, если АС=6 BD=7 CD=6. 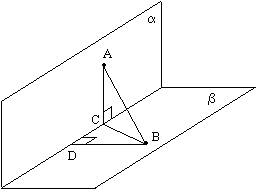 Из прямоугольного треугольника BCD найдем ВС по теореме Пифагора:
Из прямоугольного треугольника BCD найдем ВС по теореме Пифагора:ВС2=CD2+BD2 ВС2=49+36=85 Теорема: Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости. Поэтому АС перпендикулярна плоскости β, т.е. перпендикулярна любой прямой этой плоскости. АС перпендикулярна ВС. Из прямоугольного треугольника АВС найдем АВ по теореме Пифагора: АВ2=АС2+BС2 АВ2=36+85=121 АВ=11. |