| Главная Научный калькулятор | |
|
|
Задача №207Через сторону АС треугольника АВС проведена плоскость альфа, удаленная от вершины В на расстояние, равное 4 см, АС=ВС=8 см, ∠АВС=22градуса 30минут. Найдите угол между плоскостями АВС и альфа?  Треугольник АВС является равнобедренным по определению. Причем основание есть сторона АВ. Как известно в равнобедренном треугольнике углы при основании равны, поэтому ∠ВАС=∠АВС=22°30'. Пользуясь теоремой о сумме углов треугольника,
найдем третий угол треугольника:
Треугольник АВС является равнобедренным по определению. Причем основание есть сторона АВ. Как известно в равнобедренном треугольнике углы при основании равны, поэтому ∠ВАС=∠АВС=22°30'. Пользуясь теоремой о сумме углов треугольника,
найдем третий угол треугольника:∠АСВ=180°-∠АВС-∠ВАС=180°-45°=135° Определим площадь треугольника АВС, используя разные формулы: S=1/2 * АС * ВС * sin∠АСВ 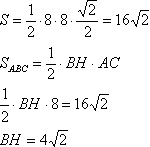 Основание высоты треугольника АВС точку Н соединим с точкой М. Прямая МН перпендикулярна АС по теореме о трех перпендикулярах (обратная). Напомним, что расстоянием от точки до плоскости является длина перпендикуляра, опущенного из этой точки на данную плоскость. Т.е. прямая ВМ перпендикулярна плоскости α, а это в свою очередь (из определения перпендикуляра к плоскости0 означает, что ВМ перпендикулярна МН. Рассмотрим прямоугольный треугольник НМВ. В нем известны катет ВМ и гипотенузы ВН. Найдем синус угла ВНМ: 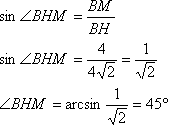
|