| Главная Научный калькулятор | |
|
|
Задача №212Дан треугольник АВС. АВ = 26, ВС = 24, АС = 10. Найти высоту, проведённую из угла С, тангенс половины угла А и расстояние между центрами вписанной и описанной окружностей. Пусть О1 - центр вписанной окружности, О - центр вписанной. Продлим биссектрису СС2 до пересечения описанной окружностью в точке Е. Проведем диаметр EF и хорды ВЕ и BF. Угол ЕВF прямой т.к. опирается на диеметр ЕF.
Пусть О1 - центр вписанной окружности, О - центр вписанной. Продлим биссектрису СС2 до пересечения описанной окружностью в точке Е. Проведем диаметр EF и хорды ВЕ и BF. Угол ЕВF прямой т.к. опирается на диеметр ЕF.Если теперь опустить перпендикуляр О1Н на сторону АС треугольника, то треугольникик О1НС и ВЕF будут подобны по двум углам (∠О1НС = ∠ВЕF = 90°; ∠АСЕ = ∠ВСЕ = ∠ЕВF - первое равенство следует из построения, второе - из теоремы о вписанных углах), откуда ВЕ:FЕ=О1Н:О1С. Обозначим радиус вписанной окружности за r, а вписанной за R, тогда EF как диаметр равен 2R и FE * О1Н = 2Rr = ВЕ * О1С Нужно отметить, что ВО1 является биссектрисой, т.к. соединяет вершину и центр вписанной окружности (центр вписанной окружности есть точка пересечения биссектрис треугольника). Треугольник ВЕО1 равнобедренный, т.к. ∠ВО1Е как внешний к треугольнику ВО1С, и ∠О1ВЕ как сумма ∠О1ВА и ∠АВЕ=∠АСЕ (опираются на равные дуги), равны 1/2(∠АСВ+∠СВА). Таким образом, ВЕ=О1Е и, значит, 2Rr = ВЕ * О1С = О1Е * О1С. Обозначим расстояние между центрами вписанной и описанной окружностей за d. Проведя через точки О и О1 диаметр КL и, используя свойство пересекающихся хорд окружности, получим: 2Rr = О1Е * О1С = О1К * О1L = (R - d)(R + d) = R2 - d2, откуда: d2 = R2 - 2Rr (3) Найдем площадь треугольника с помощью треугольник: 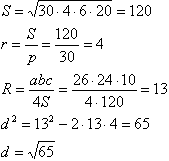 Применим теорему косинусов для нахождения косинуса угла А и формулы половинного угла и основное тождество для нохождения тангенса: 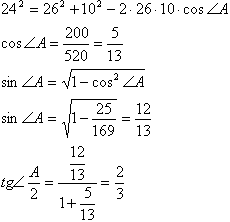
|