| Главная Научный калькулятор | |
|
|
Задача №231Дан куб ABCDA1B1C1D1 Найти угол между прямыми CD1 и AB1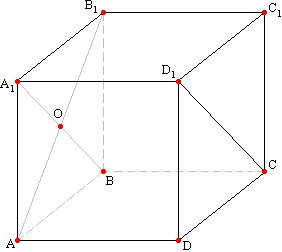 Прямые CD1 и AB1 являются скрещивающимися по определению. Углом между скрещивающимися прямыми называется угол между двумя прямыми, параллельными им и проходящими через произвольную точку. За произвольную точку примем точку О. Одна из крещивающихся прямых уже проходит через неё. Осталось сделать параллельный перенос прямой CD1. Ребра А1D1 и ВС параллельны (прямые перпендикулярные одной и той же плоскости параллельны), поэтому они определяют плоскость, причем только одну. Вспомним теорему: если две параллельные плоскости пересекаются третей, то прямые пересечения параллельны. Так, плоскость А1ВСD1 пересекает параллельные плоскости АА1В1В и СС1D1D по прямым А1В и CD1, поэтому эти прямые параллельны. Угол между прямыми А1В и АВ1 и есть искомый угол. Все грани куба квадраты. Знаем, что диагонали квадрата (как частного случая ромба) перпендикулярны. Т.е. искомый угол равен 90°. |