| Главная Научный калькулятор | |
|
|
Задача №242Угол между плоскостями n1 и n2, пересекающимися по прямой l, равен альфа. В плоскости n1 лежит прямая p, образующая с прямой l угол бета. Найдите угол между прямой p и плоскостью n2.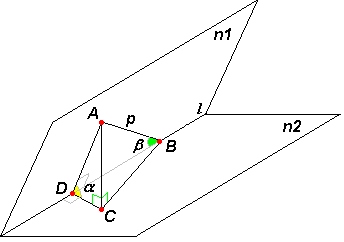 Возьмем на прямой р некую точку А и опустим из неё перпендикуляр АС на плоскость n2. Соединим точку С с В - точкой пересечения прямых р и l. Угол АВС является углом между прямой р и плоскостью n2 по определению. Опустим из точки А перпендикуляр АD на прямую l. Соединим точки С и D. Прямая CD перпендикулярна прямой l по теореме о трех перпендикулярах (обратная). Угол ADC является линейным углом двугранного угла между плоскостями n1 и n2. По данным он равен α. Вспомним связь синусов: Синус угла между прямой лежащей в одной плоскости с другой плоскостью равен произведению синуса угла между этими плоскостями на синус угла между прямой и ребром двугранного угла, о6разованного этими плоскостями. Итак: sin∠АВС=sinα * sinβ ∠АВС=arcsin(sinα * sinβ) |