| Главная Научный калькулятор | |
|
|
Задача №246Точка К - середина медианы BF треугольника АВС. Прямая АК паресекает сторону ВС в точке D. Докажите, что BD = 1/3ВС.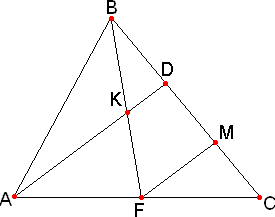 1. Выполним дополнительные построения. Параллельно прямой АК через точку F проведем прямую, которая пересечет сторону треугольника ВС в точке М. 2. Воспользуемся Параллельные и перпендикулярные прямые, применив её сначала для угла CBF (2.1), а затем для угла АСВ (2.2). 2.1. Итак, ВК=КF (по данным), значит, BD=DM 2.2. AF=FC (BF - медиана делит противоположную сторону пополам), значит, DM=MC 2.3. Из пунктов 2.1 и 2.2 делаем вывод, что BD=DM=MC, т.е. точки D и М делят сторону треугольника ВС на три равных отрезка, следовательно, BD = 1/3ВС |