| Главная Научный калькулятор | |
|
|
Задача №46Образующая конуса равна l а радиус основания равен r. Найдите площадь сечения, проходящего через вершину конуса и хорду основания стягивающего дугу в 60 градусов.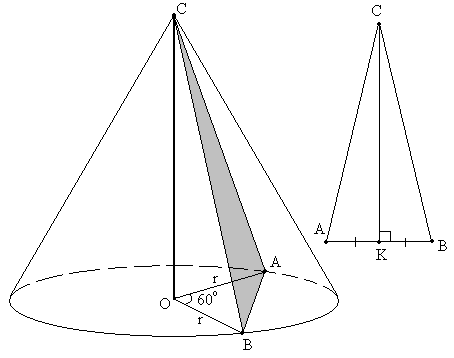 Поясним: градусной мерой дуги является центральный угол стягивающий эту дугу. Центральным называется угол, вершина которого лежит в центре окружности. Рассмотрим треугольник АВО: Мы видим, что в нем равны две стороны ОА и ОВ (то есть он - равнобедренный) и угол при вершине равен 60 градусов. Мы знаем, что у равнобедренного треугольника углы при основании равны: 2х = 180 - 60 х = 60 Иными словами все углы треугольника равны 60 градусов, а это говорит о том, что треугольник равносторонний и в нем вс стороны равны, то есть ОА = ОВ = АВ = r. В треугольнике АВС: ВС = АС = 1 - образующая конуса; АВ = r. Проведем высоту СК. Она поделит противоположную сторону попалам: АК = ВК = r/2 Теперь рассмотрим треугольник АКС: он прямоугольный и в нем АС = 1 - образующая конуса; АК = r/2. По теореме Пифагора найдем СК: 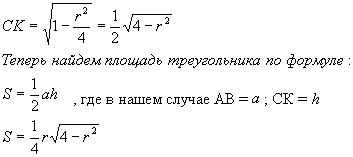
|