| Главная Научный калькулятор | |
|
|
Задача №63Квадрат вписан в ромб. Сторона квадрата параллельна диагонали ромба. Сторона ромба 6 см, угол 30 градусов.Найти площадь квадрата. 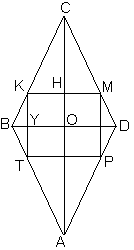 Теорема. Диагонали ромба перпендикулярны. Оспользуя эту теорему и факт того, что сторона квадрата параллельна диагонали ромба, получим: Отрезки КМ DВ и ТР параллельны между собой Отрезки КТ АС и МР параллельны между собой Отрезок АС перпендикулярен отрезкам КМ DВ и ТР Отрезок DB перпендикулярен отрезкам КТ АС и МР Треугольник КСМ равнобедренный (подобен треугольнику ВСD, который равнобедренный по данным) Теорема. Высота равнобедренного треугольника, проведенная из вершины на основание, является также и медианой основания. Значит КН = НМ = 1/2KM = 1/2KT (последнее равенство выполняется из-за равенства сторон квадрата) Аналогично из треугольника ТВК: КУ = УТ = 1/2KT = 1/2KM (последнее равенство выполняется из-за равенства сторон квадрата). Следовательно КУ = КН. Теорема. Если в прямоугольнике две смежные стороны равны, то такой прямоугольник является квадратом. Значит, прямоугольник КНОУ - квадрат. Надо заметить, что ОН = КУ = 1/2КТ Обозначим половину стороны квадрата за х (КН = НМ = КУ = УТ = ОН = х) Из треугольника АВС определим сторону АС (и её половину) по теореме косинусов: 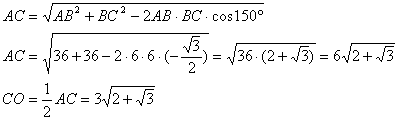 И теперь по теореме Пифагора из треугольника ОВС найдем ОВ: 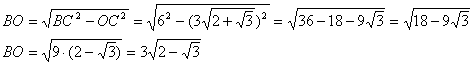 Надо заметить, что СН = СО - ОН Прямоугольные треугольники ВОС и КНС подобны по острому углу (угол ВСО). Запишем равные соотношения: 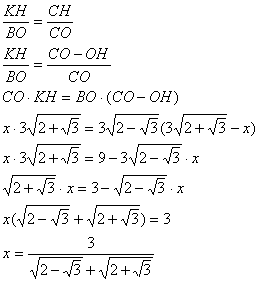 Помним, что х - это половина стороны, тогда площадь квадрата равна: 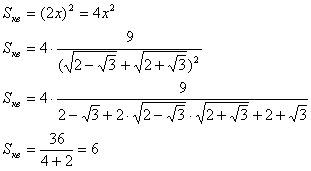
|