| Главная Научный калькулятор | |
|
|
Задача №64Дан параллелограмм АВСD, в котором диагонали АС = 10см и ВD=6см. Точки К,L,M,N являются соответственно серединами сторон параллелограмма АВ, ВС, CD и AD.Найти периметр KLMN. 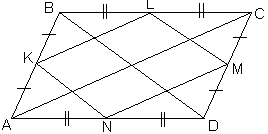
Рассмотрим треугольник АВС (АСD) в нем KL (MN) является средней линией. Теорема. Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третей стороне и равна её половине. Откуда KL = MN = 1/2АС = 5. Рассмотрим треугольник ВСD (АВD) в нем LМ (КN) является средней линией. Значит, LМ = КN = 1/2BD = 3. Вычисляем периметр: Р = KL + MN + LМ + КN = 5 + 5 + 3 + 3 = 16. Кстати, эта задача дает почву для теоремы: Периметр параллелограмма, вершины которого лежат на серединах другого параллелограма, равен сумме диагоналей другого параллелограмма. |