В треугольнике АВС биссектриса АЕ равна отрезку ЕС. Найти углы АВС, если АС=2АВ

Решение:

1) Достроим треугольник до треугольника АСМ, добавив равный ему,  где АВ=ВМ, СМ=АС. Тогда СМ=АМ=АС, и треугольник АСМ - равносторонний (т.к. АС=2 АВ).
Все углы равностороннего треугольника равны 60º 
∠САВ=60º
АЕ- биссектриса, и ∠ САЕ=∠ЕАВ=∠АСЕ=30º, а ∠ СВА=180º-(60º+30º)=90º
-
2) В равнобедренном треугольнике АЕС ( по условию) 
проведем высоту ( медиану) ЕН.  
АН=НС=АВ 
В треугольниках ЕАН и ЕАВ 
∠НАЕ=∠ЕАВ по условию 
АН=АВ 
сторона АЕ - общая 
Треугольники НАЕ и ЕАВ равны по первому признаку.  
∠ ЕНА= ∠ЕНС=90º по построению 
Отсюда угол АВЕ=АНЕ=90º 
Треугольник АВС - прямоугольный с прямым углом В 
Сумма  острых углов прямоугольного треугольника равна 90º  
∠ ЕАС=∠ЕСА ⇒ 
Так как АЕ биссектриса ∠ВАС, то ∠ВАС=2∠АСВ 
∠ АСВ+∠САМ= 3 ∠ АСВ 
∠ АСВ=90º:3=30º 
∠ САВ=2∠САВ=60º
-
3)
 АЕ=СЕ, следовательно, треугольник АСЕ - равнобедренный, угол САЕ=АСЕ. Достроим треугольник АВС равным ему, где боковая сторона равна АС, а основание равно АВ.
Тогда в нем АЕ=ЕС, и ЕС является биссектрисой угла С.
В новом треугольнике биссектрисы точкой пересечения делятся на равные части ( считая от вершин).
АВ=1/2АС, а основание нового треугольника равно АС, боковые стороны тоже в нем равны.
Так как АС=2АВ, ∠ АСВ=30°, отсюда ∠ВАС=60°.
Треугольник АВС - прямоугольный с прямым углом В.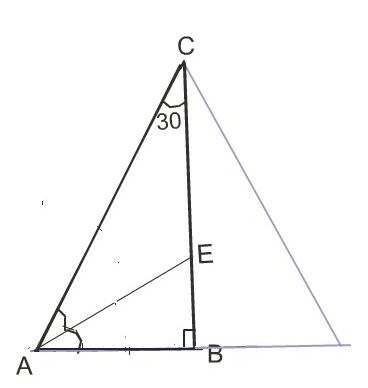