Прямая задана уравнением 2x+5y-10=0 а)Запишите координаты пересечения прямой с осями координат.


Главная Научный калькулятор
Меню Алгебра Геометрия Основные понятия Аксиомы планиметрии Углы Перпендикулярные и параллельные прямые Перпендикуляр и наклонная Круг (окружность) Треугольник Четырехугольник Параллелограмм Трапеция Многоугольники Основные понятия стереометрии Аксиомы стереометрии Прямые в пространстве Пересекающиеся прямые Параллельные прямые Скрещивающиеся прямые Прямая и плоскость в пространстве Перпендикулярность прямой и плоскости Параллельность прямой и плоскости Угол между прямой и плоскостью Теорема о трех перпендикулярах Формула двойного проектирования Плоскости в пространстве Пересекающиеся плоскости Параллельность плоскостей Перпендикулярность плоскостей Площадь проекции плоской фигуры на плоскость Многогранники: Пирамида Призма Тела вращения: Цилиндр Конус Шар (Сфера) Объем тел вращения Задачи по геометрии Примеры решений Вспомогательные материалы: Таблицы Брадиса Исследование функций Асимптоты. Первая производная. Вторая производная. Графики функций Задачи по функциям Тригонометрия Тригонометрические неравенства	Треугольник : Равнобедренный треугольник : Прямоугольный треугольник : Четырехугольник : Параллелограмм : Ромб : Прямоугольник : Трапеция : Многоугольники : Круг и окружность : Прямые и плоскости : Пирамида : Системы координат : Цилиндр : Конус : Углы : Призма : Параллелепипед : Сфера и Шар : Построения Прямая задана уравнением 2x+5y-10=0 а)Запишите координаты пересечения прямой с осями координат. Б) Найдите площадь треугольника, образованного осями координат и этой прямой. Решение: 2x + 5y -10 = 0 5y = -2x +10 y = -0.4x + 2 при пересечени прямой y = -0.4x + 2 с осью Y, x = 0. При пересечени прямой y = -0.4x + 2 с осью X, y = 0. Составим две системы: 1) y = -0.4x + 2 2) y = -0.4x + 2 y=0 x = 0 y =0 x = 0 x = 5 y = 2 Ответ: (5;0) Координаты пересечения с осью X Ответ: (0;2) Координаты пересечения c осью Y Треугольник образованный осями координат и этой прямой прямоугольный. 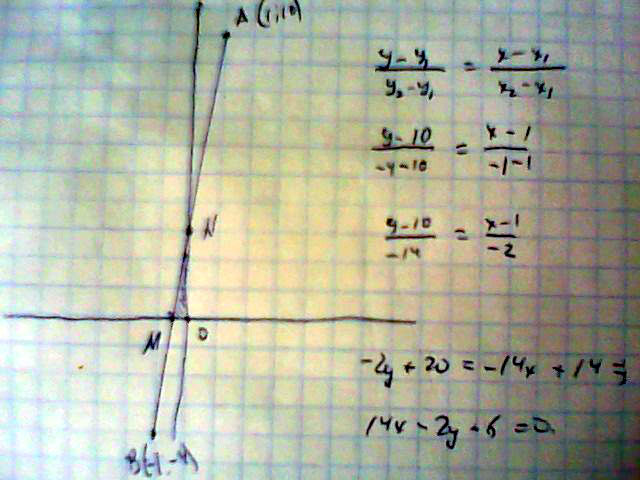Значит его площадь равна половине произведения катетов его катетов(s = (x+y)/2) S = (52)/2 = 5 площадь треугольника Прямая проходит через точки А(1;10) и В(-1;-4). Найдите площадь треугольника, ограниченного этой прямой и осями координат Найдем уравнение прямой АВ по формуле (у-у1)/(у2-у1)=(х-х1)/(х2-х1), (у-10)/(-1-10)=(х-1)/(-1-1); 14х-2у+6=0, Определим координаты пересечения прямой АВ с осями координат. х=0; 2у=6; у=3; Точка N(0;3). у=0; 14х=-6; х=-3=7. Точка М(-3/7; 0). ΔМNО- прямоугольный. Вычислим его площадь S=0,5·(3/7)·3=9/14 см². Ответ: 9/14 см². Найти площадь треугольника, образованного осями координат и прямой АС, где А(0;-3) С(3;4) Уравнение прямой по двум точкам имеет следующий вид, (у-у1)/(у2-у1) = (х-х1)/(х2-х1) подставляем координаты наших точек А и С и получаем уравнение: 3у + 9 = 7х или у = (7/3)х - 3 находим точку пересечения прямой АС с осью Ох, для этого подставляем в уравнение у =0 (7/3)х - 3 = 0 х = 9/7 треугольник прямоуг. (т.к. Образован осями координат) соответственно ели мы знаем точки пересечения АС и осями, то можем узнать длину его катетов: 3 и 9/7 площадь = 1/2 3 * 9/7 = 27/14 Прямая проходит через точки А(1;-1) и В(-3;2). Найдите площадь треугольника ограниченного этой прямой и осями координат Уравнение прямой у=kx+b Чтобы найти коэффициенты k и b подставим координаты точек А и В в это уравнение: -1=k·1+b ⇒ b=-k-1 2=k·(-3)+b 2=-3k-k-1 3=-4k k=-3/4 b=-3/4-1 b=-1 целая 3/4=-7/4 Прямая у=-(3/4)х- (7/4) Эта прямая пересекает ось ох в точке у=0 х=-7/3 ось оу в точке х=0 у=-(7/4) Площадь треугольника, ограниченного прямой и осями координат- прямоугольный. Площадь прямоугольного треугольника равна половине произведения катетов S=(1/2)·(7/3)·(7/4)=(49/24)=2 целых 1/24 кв.ед. Найти площадь треугольника, ограниченного прямой y-x-3=0 и осями координат Раз треугольник ограничен осями координат, то он будет прямоугольным(начало координат - О, прямой угол этого треугольника) найдем пункты пересечения прямой (обозначим ее АВ), уравнение которой 5х - 3у - 15 = 0. с осями с осью абсцисс у= 0 5х -30 - 15 = 0 5х=15 х=3 А(3;0) ⇒ длина катета АО =3 с осью ординат: х = 0 50 - 3у - 15 = 0 -3у=15 у=-5 В(0;-5)⇒ длина катета ВО равна 5 Sabo = BO * AO * 1/2 = 53 1/2 = 7,5 При каких значениях р прямая y=px+2 образует с осями координат треугольник, площадь которого равна 64? Прямая пересекает ось 0У при х=0 в точке р×0+2=2. Прямая пересекает ось0Х при у=0 в точке 0=рх+2; х=\( \frac{-2}{p} \) У нас получился прямоугольный треугольник, площадь которого равна: \( \frac{1}{2} \)×2×х=64; х=64 Этот треугольник может лежать по разные стороны от оси 0У⇒х может быть как положительной координатой, так и отрицательной. Рассмотрим первый случай: \( \frac{-2}{p} \)=64; р=-0,03125(или -\( \frac{1}{32} \). Рассмотрим второй случай: \( - (\frac{-2}{p})=64 \); \( \frac{2}{p}=64 \); р=0,03125( или \( \frac{1}{32} \)). Ответ: -0,03125; 0,03125. Прямые заданы уравнениями 3х+2у-9=0, у+3=0 а) Начертите эти прямые в одной системе координат б) Найдите координаты точки пересечения этих прямых в) Найдите площадь треугольника, образованными этими прямыми и осью ординат. 1. Выразим у через х. 3х+2у-9=0, у = -1,5х + 4,5 у+3=0, у = -3 Чтобы построить эти прямые, нужно 1) на координатной плоскости отметить точку у = -3 и восстановить в этой точке перпендикулярную прямую, параллельную оси Ох. 2) отметить две точки: А(1; 3) и В (3;0). 3) провести через эти точки прямую АВ. 2. -1,5х + 4,5 = -3, х = 5. Подставим это значение в уравнение прямой и найдем ординату точки пересечения: у = -1,55 + 4,5 = - 3. Координаты точки пересечения равны (5; -3). 3. Треугольник, площадь которого нам нужно отыскать, прямоугольный, длины его катетов равны 5 (абсцисса точки пересечения) и 4,5 (ордината точки пересечения прямой у = - 1,5х + 4,5 с осью ординат) + 3 = 7,5. Следовательно, его площадь, равная половине произведения катетов, будет равна 57,5/2 = 18.75 кв.ед.