Изобразить систему координат Oxyz точку А(1,2,4). Найти расстояние от этой точки до координатных плоскостей.

Решение:

Расстояние от точки до координатных плоскостей равно координате по модулю, которая не используется в названии плоскости.

Расстояние до плоскости Oxy  равна координате |z| точки А т.е. 4 

Расстояние до плоскости Oyz равна координате |x| точки А т.е. 1 

Расстояние до плоскости Oxz равна координате |y| точки А т.е. 2 

Изобразите систему координат и постройте точку М (1;-2;-4) найти растояние от этой точки до координатных плоскостей

Приблизительно так, точки относятся к трем плоскостям. А найт растояние до плоскости это найти расстояние до любой точки этой плоскости. Ну и если по прямой, то берутся те же координаты, только соответствующая равна 0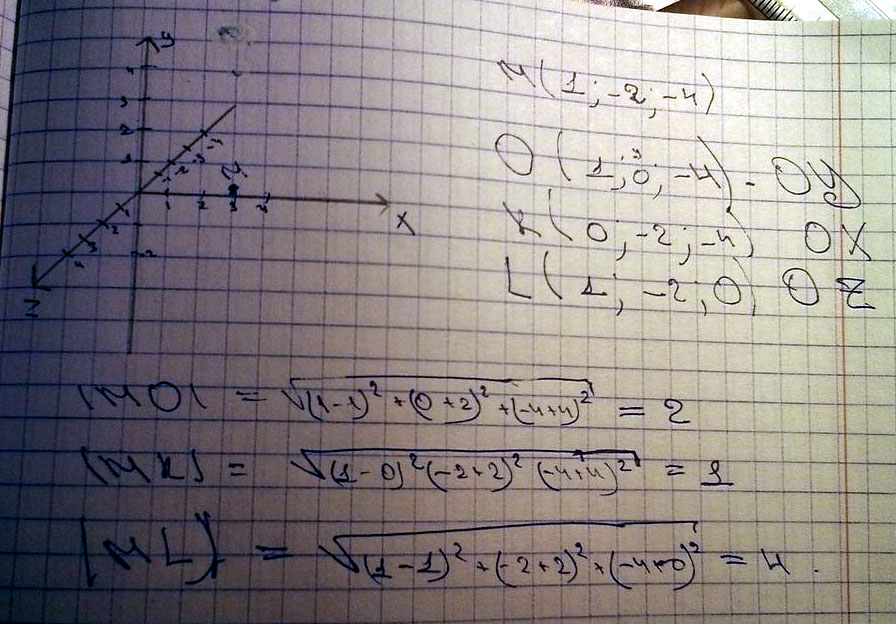

---

Изобразите систему координат Oxyz и постройте точку A(1; —2; -4). Найдите расстояние от этой точки до координатных плоскостей
от А до ху расстояние 4 (равно модулю координаты по оси z)
от А до хz расстояние 2(равно модулю координаты по оси y)
от А до yz расстояние 1(равно модулю координаты по оси x)

1. На оси х сдвигаемся на 1 единицу в положительном направлении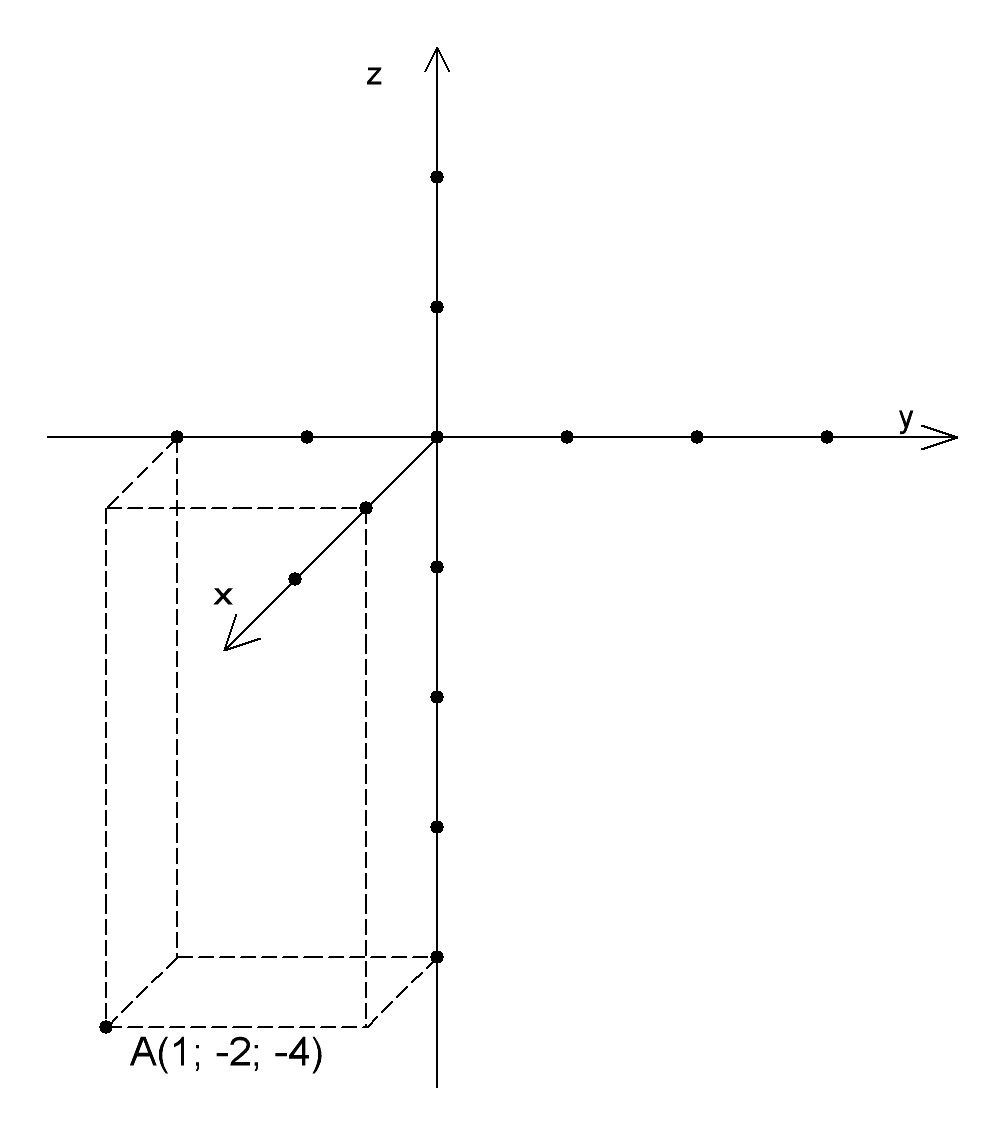
2. Через текущую точку (точку, в которой находимся в данный момент) (1; 0; 0) проведем прямую, параллельную оси у - обозначим ее у`
3. На оси у` сдвигаемся на 2 единицы в отрицательном направлении
4. Через текущую точку (1; -2; 0) проведем прямую, параллельную оси z - обозначим ее z`
5. На оси z` сдвигаемся на 4 единицы в отрицательном направлении. Получим искомую точку А(1; -2; -4)
При построении мы сдвинулись по оси х на 1 единицу - значит расстояние до плоскости yOz равно 1. Аналогично, сдвиг по оси y||y` на 2 единицы - расстояние до плоскости xOz равно 2, сдвиг по оси z||z` на 4 единицы - расстояние до плоскости xOy равно 4