Запишите уравнение окружности с центром в начале координат и проходящей через точку M(12;-5).

Решение:

Уравнение окружности, с центром в начале координат:

\( x^{2} + y^{2} = r^{2} \)

что бы найти радиус, рассмотрим прямоугольный треугольник с катетами 12 и 5 (так как точка лежит на окружности)

\( r^{2} = 12^{2} + 5^{2} = 144+25 = 169 \)

Радиус окружности равен 13, но так как в формуле он нужен в квадрате, то извлечение не требуется.

Уравнение: \( x^{2} + y^{2} = 169 \)

В прямоугольной системе координат треугольник ABC задан координатами своих вершин A(1; 3), B(1;-3), C(-3;0). Напишите уравнение окружности, описанной около этого треугольника.

Найдем координаты центра описанной окружности \( (x,y) \) и радиус \( r \), решив систему

\( \begin{cases} (x-1)^2+(y-3)^2=r^2\\ (x-1)^2+(y+3)^2=r^2\\ (x+3)^2+y^2=r^2 \end{cases} \)

Вычитая из второго уравнения системы первое, получаем \( (y+3)^2-(y-3)^2=0 \), так что \( y=0 \). Подставив найденное значение, будем иметь:

\( \begin{cases} (x-1)^2+9=r^2\\ (x+3)^2=r^2 \end{cases} \)

Опять вычтем из второго уравнения первое, тогда \( x=1/8 \). Наконец, \( r=25/8 \) и искомое соотношение

\( (x-1/8)^2+y^2=(25/8)^2 \)

Запишите уравнение окружности, касающейся осей координат и проходящей через точку (8; -4)

Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство\( |x_0|=|y_0|=R; \) учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти) \( x_0=-y_0=R \)

уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2

\( (8-R)^2+(-4+R)^2=R^2;\\ R^2-16R+64+R^2-8R+16=R^2;\\ R^2-24R+80=0;\\ (R-20)(R-4)=0 \);

R=20 или R=4

значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат

\( (x-20)^2+(y+20)^2=400 \)

и \( (x-4)^2+(y+4)^2=16 \)

Составьте уравнение окружности, проходящей через начало координат и точки (6;0) и (0;8)

уравнение окружности x^2 + ax + y^2 + by = c. 

Если проходит через начало координат, то

0 + 0 + 0 + 0 = c и c=0.

Т. К. Окружность проходит через (6,0), то

36 + 6a + 0 + 0 = 0, a=-6.

Т. К. Окружность проходит через (0,8), то

0 + 0 + 64 + 8b = 0

b=-8.

Получаем уравнение окружности x^2 - 6x + y^2 - 8y = 0

Уравнение окружности имеет вид \( (x-x_o)^2+(y-y_o)^2=R^2 \)

так данная окружность проходит через точки (0;0), (6;0), (0;8), то

\( (0-x_o)^2+(0-y_0)^2=R^2;\\\\(6-x_o)^2+(0-y_o)^2=R^2;\\\\(0-x_o)^2+(8-y_o)=R^2; \)

откуда

\( x^2_o=(6-x_0)^2; \)

\( x_0=6-x_0;x_{0(1)}=3;\\\\x_0=x_o-6;0=-6 \)

\( x_o=3; \)

\( y^2_o=(8-y_0)^2; \)

\( y_0=8-y_0;y_{0(1)}=4;\\\\y_0=y_o-8;0=-8 \)

\( y_o=3; \)

\( R^2=x^2_o+y^2_o=3^2+4^2=9+16=25; \)

уравнение окружности имеет вид

\( (x-3)^2+(y-4)^2=5; \)

Запишите уравнение окружности с центром в начале координат через точку А(-2;4)

Если точка (-2;4) принадлежит графику, то радиус окружности равен расстоянию от этой точки до начала координат.  

Сторона АС=2, ВС=4, по теореме Пифагора АВ=sqrt(20)

тогда уравнение окружности будет выглядеть так:

20=x^2+y^2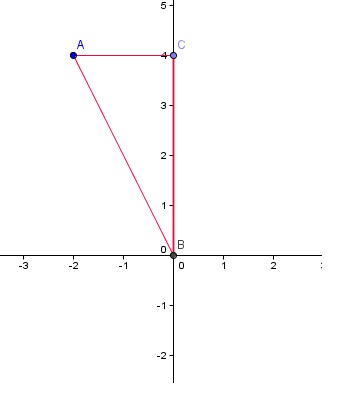

Запишите уравнение окружности, проходящей через начало координат и точку А(6;0), если известно, что радиус окружности равен 3(корень из 2), центр лежит на прямой у=х

Уравнение окружности имеет вид (х - х0)^2 + (y - y0)^2 = R^2, где центр имеет координаты (х0; у0) и R - радиус окружности. Подставляем в данной уравнение координаты точки А, получаем (6 - х)^2 + (0 - y)^2 = 18. Так как центр принадлежит прямой у = х, то заменяем у на х:
(6 - х)^2 + (0 - х)^2 = 18, откуда х = 3.
Центр данной окружности лежит в точке О (3;3)
Следовательно, искомое уравнение окружности можно записать в виде
(х - 3)^2 + (y - 3)^2 = 18

Напишите уравнение окружности с центром в точке (-3;4), проходящей через начало координат

Уравнение окружности имеет вид (x – a)2 + (y – b)2 = R^2, где a и b – координаты центра A окружности.  Подставим координаты центра (-3;4) в уравнения и получим: (x+3)+(y-4)=R^2   Осталось только найти R

Найти его очень легко. Начертим координатные оси на листке, и обозначим точку А с координатами (-3;4). В условии задачи сказано, что окружность проходит через начало координат, следовательно расстояние от точки А до начала координат и есть искомый радиус.

Далее опускаем проекции точки А на оси 0x и 0y. Рассматриваем прямоугольный треугольник, в котором нам известны два катета, имеющие длины 3 и 4, и по теореме Пифагора найдём гипотенузы(т. Е R).

R=квадратный корень из(16+9)=5; подставив радиус в уравнение получаем:

(x+3)+(y-4)=25

1) Составьте уравнение окружности, которая касается оси Оу в точке (0: - 2) и имеет радиус, равный 2/3 => ( Две третьих столбиком см )
2) Выясните, имеет ли окружность \((х - 3)^2 + (у + 1)^2 = 1\) общие точки с осью абсцисс. Найдите их координаты

1) B(0; -2) R=\( \frac{2}{3} \)
Если построить координатную прямую, то на ней будет два центра окружности
A₁ \( (- \frac{2}{3}; -2) \)
A₂ \( (\frac{2}{3}; -2) \)
Получится два уравнения
\( (x+ \frac{2}{3} )^{2} +(y+2)^{2} =(\frac{2}{3})^{2} \)
\( (x- \frac{2}{3} )^{2} +(y+2)^{2} =(\frac{2}{3})^{2} \)
2) предположим, что окружность имеет с осью абсцисс общие точки и найдем их при y=0
уравнение принимает вид (x-3)²+(0+1)²=1
(x-3)²+(0+1)²=1
(x-3)²+1-1=0
x²-6x+9=0
Д=36-36=0
\( x= \frac{6}{2} =3 \)
Ответ: координаты точки (3;0)

Напишите уравнение окружности а) с центром в точке О (2;3) И R=4, б) с центром в начале координат и R=5

(х-а)²+(у-в)²=R²- уравнение окружности где (а; в)-координаты центра окружности R-радиус
(х-2)²+(у-3)²=4²
(х-2)²+(у-3)²=16
начало координат имеет координаты О(0;0)
(х-0)²+(у-0)²=(5/2)²
x²+y²=25/4  (R=5/2)       X²+y²=25 (R=5)

Напишите уравнение окружности с центром в точке P(-2;-1), если она проходит через точку Q(1;3)

Уравнение окружности : (х-х0)^2 + (у-у0)^2 =R^2
центр окружности Р(-2;-1), подставим ее координаты в уравнение
(х+2)^2+(у+1)^2=R^2
теперь осталось найти радиус
найдем длину вектора PQ:
PQ{3;4}, |PQ|=корень из(3^2+4^2)=5
именно длина вектора PQ для нас является длиной радиуса окружности
конечный вид уравнения окружности:
(х+2)^2+(у+1)^2=25

Задана окружность (х – 1)2 + (у – 2)2 = 1. Запишите уравнение окружности, в которую переходит данная окружность при повороте на угол 90° против часовой стрелки около начала координат.
Гомотетия с центром в начале координат переводит точку А(2; – 4) в точку В(1; – 2). Найдите коэффициент гомотетии.

У данной окружности центром является точка (1;2). При повороте вокруг начала координат против часовой стрелки точка (х; у) переходит в точку (-у; х). Центр будет (-2;1). Радиус не изменится.  
Получится окружность (х+2)²+(у-1)²=1.
2. При гомотетии с центром в начале координат точка (х; у) переходит в точку (кх; ку). Для нахождения  коэффициента гомотетии делим 1/2 =0,5 или -2/(-4) = 0,5. Это и есть коэффициент гомотетии.

Запишите уравнение окружности, касающейся осей координат и проходящей через точку (8;-4) (-9;2)

Через формулу (x - R)^2 + (y - R)^2 = R^2

короче: (-9-8)^2+(-9-2)^2= (-17)^2+(-11)^2=289+121=410

Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти) 

уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2R=20 или R=4значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат

Составьте уравнение окружности касающейся осей координат и проходящей через точку К (2;1)

Если окружность касается осей координат, то её центр находится на биссектрисе прямого угла между осями координат (х = у) и радиус R равен х.
В уравнении окружности можно у и R заменить на х.
Записываем уравнение окружности:
(х-2)²+(х-1)² = x².
x²-4x+4+x²-2x+1 = x².
Получаем квадратное уравнение:
х²-6х+5 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-6)^2-4*1*5=36-4*5=36-20=16; Дискриминант больше 0, уравнение имеет 2 корня:    
x₁=(√16-(-6))/(2*1)=(4-(-6))/2=(4+6)/2=10/2=5;    x₂=(-√16-(-6))/(2*1)=(-4-(-6))/2=(-4+6)/2=2/2=1.    
Найдены 2 точки, которые могут быть центрами заданных окружностей.
Ответ: (х-5)²+(у-5)² = 25.
  (х-1)²+(у-1)² = 1