Отрезки АС и BD пересекаются в середине О отрезка АС, угол ВСО = углу DAО. Докажите, что треугольник ВОА = треугольнику DOC

Решение:
1) Треугольники АОД и СОВ равны по стороне (АО=ОС) и прилежащим к ней углам (пара данных и пара вертикальных) => ВО=ОД. 2) Тогда в четырехугольнике АВСД диагонали пересекаются в т.О и ею делятся пополам, значит это параллелограмм, а в параллелограмме треугольники АОВ и СОД равны.

---

Поскольку угол ДАО=ВСО, то  углы ВАО и ДСО равны, т.к. являются смежными с углами Дао и Всо.  Поскольку отрезки Ас и Вд пересекаются в точк О и делят отрезок АО пополам, то АО= ОС. Углы ВОС и СОД равны как вертикальные. Следовательно треугольники ВОА и дОС равны по стороне и прилежащим у ней углам!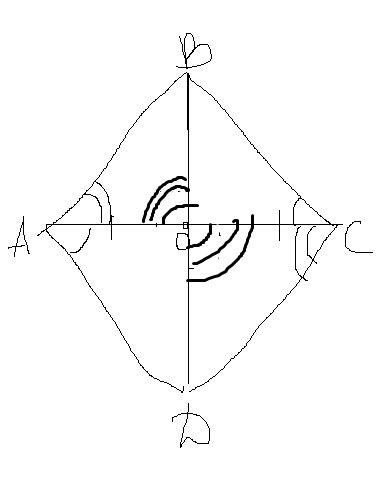