Расстояние между параллельными гранями шестигранной головки болта, верхнее основание которого имеет форму правильного шестиугольника, равно 1,5 см. Найдите площадь верхнего основания

Решение:

Строну можно найти, например, из теоремы косинусов:

1,5^2=2a^2(1-cos120)=2a^2*1.5

2a^2=1.5

a^2=3/4

S=6*(a^2*sqrt3/4)=6*3/4*sqrt3/4=9sqrt3/8

(площадь 6-угольника= 6 маленьких равносторонних треугольника)

шестигранник разделим не 6 треугольников, причем 1.5 см - это будет диаметр вписанной окружности. Тогда радиус вписанной окружности = 0,75 см.

Рассмотрим один такой треугольник.

Угол при центре окружности равен 360/6=60 град, значит треугольник равнобедренный, тогда углы при основании = (180-60)/2=60град - значит треугольник равносторонний, тогда радиус описанной окружности - высота этого треугольника и биссектриса для угла при центре окружности, тогда углы в таком треугольнике будут 30, 60, 90, значит

Пусть гипотенуза  - 2х, тогда один катет, напротив угла60=0,75, а второй катет напротив угла 30=половина гипотенузы=х, тогда

по т Пиф \( 0,75^{2}=4x^{2}-x^{2} \)

\( 0,5625=3x^{2} \)

\( x=\sqrt(0,5625/3)=\sqrt(0.1875)=0.25\sqrt3 \)

Тогда площадь шестиугольника=\( 1/2*6*0,75*0.25\sqrt3=0,5625\sqrt3 \) см квадратных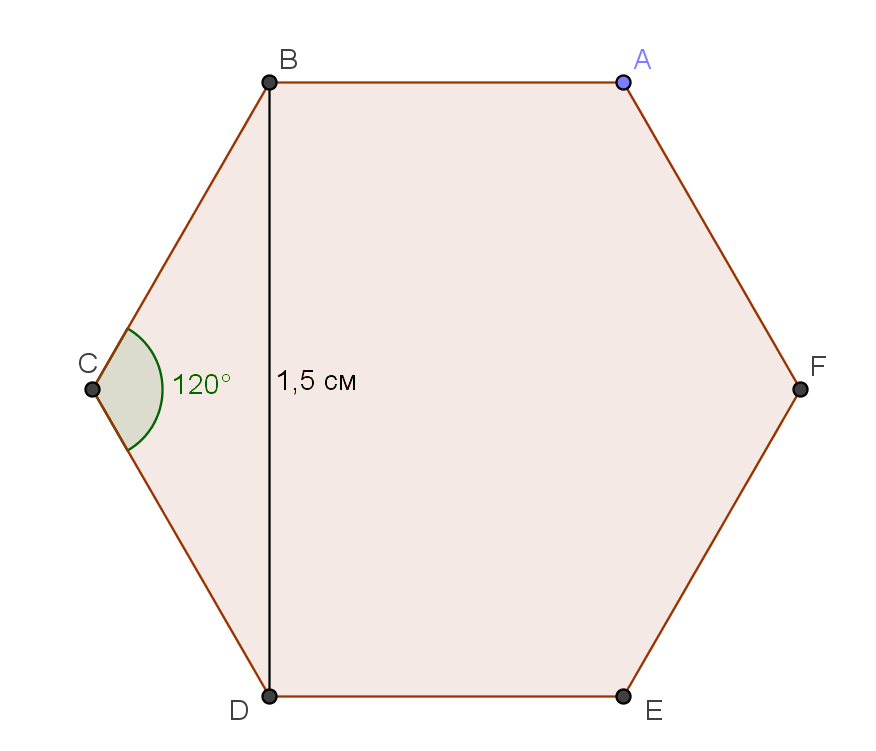