В прямоугольный треугольник вписана окружность. Точка ее касания с гипотенузой делит гипотенузу на части, длины которых равны 6 см. И 4 см. Вычислите радиус окружности?

Решение:
Точка касания с гипотенузой ВС является точка Е (СЕ=4, ВЕ=6), с катетом АС точка К, с катетом АВ точка М. Угол А прямой. СЕ=СК=4, длины отрезков выходящих из одной вершины до точек касания к      окружности равны, по этому же правилу ВЕ=ВМ=6 Центр окружности О, r-радиус окружности. ОК=ОМ=r и ОК перепендик АС, ОМ перпендик АВ. АМОК-квадрат и АМ=АК=r Тогда АС=r+4, АВ=r+6, ВС=4+6=10 по теореме Пифагора ВС^2=АС^2+АВ^2 10^2=(r+4)^2+(r+6)^2 r^2+8r+16+ r^2+12r+36=100 2r^2+20r+52=100 2r^2+20r-48=0 сократим все на 2 r^2+10r-24=0 найдем дискрим. Д=100+96=196 корень из Д=14 r1=(-10+14)/2 r1=2 r2=(-10-14)/2=-12(радиус не может быть отрицат.) Радиус вписан.окружности равен r=2см

---

т.О - центр окружности вписанной в треугольник. так как окружность касается сторон треугольника, то радиус этой окружности находиться под прямым углом к каждой стороне получилось три пары треугольников: BKO и BLO; CLO и CMO; AMO и AKO - которые равны между собой как прямоугольные треугольники (за катетом - то наш радиус и гипотенуза - это общая сторона) таким образом BK=Bl=6; CL=CM=4; AM=MO=AK=KO=r; теперь основываясь на теореме Пифагора AB2+AC2=BC2 (r+6)2+(r+4)2=102 решаем квадратное уравнение и находим радиус r=2 (второе решение уравнения отрицательное, а значит нам не подходит) :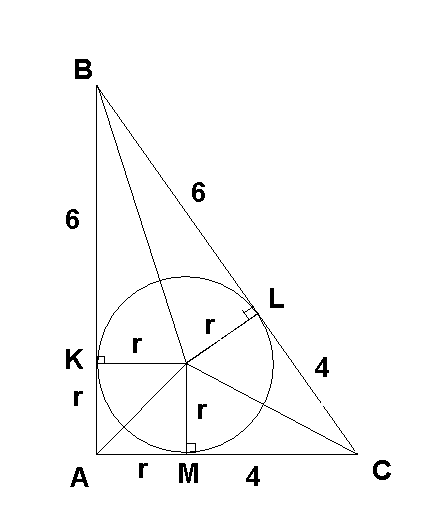