В произвольном треугольнике АВС, АВ = 3, ВС = 7, Медиана ВD = 4. Найти АС и площадь треугольника АВС

Решение:
1) По формуле медианы тр-ка: ВD^2=(2(CB^2+AB^2)-FC^2)/4. Подставим известные данные. Получим: 16=(116-AC^2)/4 => 116-AC^2=64 => AC^2=52 => AC=2*sqrt(13) 2) Нахождение площади по формуле Герона смотри в прикрепленном файле

Достроим АВС до паралеллограмма(продлить медиану на свою длину ) и воспользуемся формулой: Сумма квадратов 2 диагоналей рана удвоенной сумме квадратов сторон паралеллограмма. Пусть вторая диагональ х. 2(3*3 + 7*7) = х*х +(4+4)(4+4) 112=64+х*х х*х=52 х=2корня из 13       Площадь находиться по герону: Корень квадратный из (р(р-а)(р-в)(р-с))=6корней из 3. Ответ: 3 сторна равна 2 корня из 13,       площадь равна 6 корней из 3.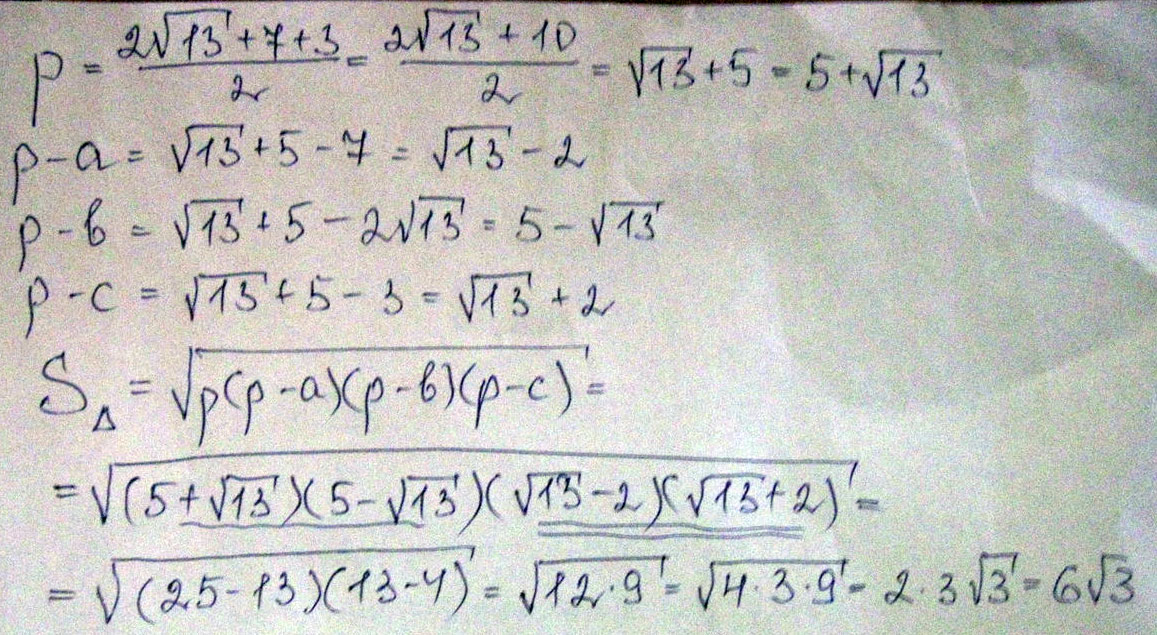